グラフの中心でAIを叫んだノード(なおAIは出ない) 〜あるいはnode2vecに至るグラフ理論〜
1 イントロダクション
本記事を読む前に、本章を読んでください。書いていくごとに、とにかくボリュームが多くなりました。
本章では「グラフとは何か?」と「本記事で扱うこと・扱わないこと」をまとめています。非常にボリューミーなので、自身の必要な知識・不要な知識を取捨選択して読んでいただくことをお勧めします。
1.1 そもそもグラフ理論とは
まず第一に、 グラフ理論は図示とは全く別のもの です。
恥ずかしながら、ある勉強会でグラフ理論のタイトルで話す登壇者の方がいて「より良い図示の方法をまとめたトークかなにかかな。」と思っていました(無事、話を聞いて「あぁ、そっちね。」となりました)。
本ブログの著者ふたりとも物理出身の門外漢故広い心で見守ってくれればと思います。
グラフ理論とは相互に関係し合うネットワークを数学的に扱う一学問です。
下記のようなシンプルなグラフネットワークの例を考えます。例えばECサイトにおいてユーザーが商品ページを閲覧します。その際の商品をノードに、ページ遷移をエッジとしてグラフを構築します。

Figure 1: グラフの例
例えば、上記グラフで商品 \(u_2\) を閲覧したユーザーは、商品 \(u_1,\ u_3,\ u_7\) に遷移するエッジ(学習データとしてのユーザーの閲覧履歴)が存在します。集計ベースの共起確率に基づく商品レコメンドでは、商品 \(u_2\) を見ているユーザーには商品 \(u_1,\ u_3,\ u_7\) ばかりがオススメされることになります。ですが、グラフ理論に基づきネットワークを考慮すると商品 \(u_1,\ u_7\) を見ているユーザーは共通して商品 \(u_8\) を閲覧しているので、商品 \(u_8\) も 見えないエッジ としてレコメンドすることができるようになるわけです。
このような集計ベースではできないニュアンスが表現できるグラフ理論に可能性を感じ勉強を始めた次第です。
次章にて数学的なグラフの扱いについて解説します。続く章では、グラフの機械学習を用いたアプローチを紹介します。
1.2 近年の進展
グラフ理論というよりネットワーク科学の枠組みに近いようには思いますが、面白い内容として「新型インフルエンザ(H1N1型)大流行の予測」に言及します。記憶に残っている方もいるかと思いますが、2009年に新型インフルエンザが流行しました。当時の世界中の交通機関ネットワークの構造と動態から新型インフルエンザの流行予測がされました(結構リンクの動画が面白いので見ることをオススメ)。通常のインフルエンザが流行する1,2月とは異なり、本予測では2009年の10月にピークを迎えると予想されました。通常のインフルエンザの流行に合わせてワクチンを11月に間に合わせるために開発が行われていたそうなのですが、予測により開発の意味がなくなってしまうことが示されました。世界で初めての感染症の正確なリアルタイム予測の例になったようです。
上記はグラフ理論としてのアプローチの成功例の一つでしたが、近年機械学習に関連する国際会議などでグラフに関する論文数も爆発的に増えて来ており客観的にも注目度がわかります[1]。盛んに研究が進む理由は以下の2点あると個人的には考えています。
- 実際のビジネス領域への活用の幅の広さと発想の容易さ
- 近年の機械学習手法の発展に伴う、新しい解析方法の開発
それぞれの項目ごとに簡単に触れて行きます。
1.2.1 ビジネス活用
上記で紹介した通り、グラフ理論では相互に関係し合うネットワーク構造を扱います。このようなネットワーク構造は実生活で非常に多く登場し、多くの問題をグラフの枠組みに落とし込んで考えることが可能です。手元で思い浮かぶだけでも以下のように多くの項目があります。
- ソーシャルネットワークでの相互フォロー関係
- 論文の共著者
- 会社などの組織内での情報の共有ネットワーク(重要な人物などをを知る)
- サプライチェーン
- インターネットなどに代表される通信ネットワーク
- 不正アクセスの検知
- 電力網
- お金の取引ネットワーク
- 交通ネットワーク(乗り換え案内)
- 道路と車の交通渋滞予測
- 新しいタンパク質の構造予測
- 有毒化合物の発見や創薬
- 脳内の電子信号網(ニューロン)
- ニューラルネットワークの構造
- 病気などの感染現象(上記H1N1の流行)
- 自然言語処理
- 画像処理
様々なネットワークごとに各々のタスクはあるものの、それぞれグラフ理論という枠組みに落とし込みアプローチすることができます。
FacebookやTwitterの「友達かも?」機能や公共交通機関の「乗り換え案内」などはもちろんですが、日本の企業でもメルカリのプレスリリース(メルカリ、英ブリストル大学、東北大学との 共同研究成果を国際会議で発表 〜ネットワーク解析を用いた不正取引検出〜)や、富士通の富士通のAI(人工知能)技術「FUJITSU Human Centric AI Zinrai」にもグラフデータの探索機能があるようです。日本の事例はどちらも不正アクセスや不正取引の発見を目的としているようです。
著者自身の知識が足りずあまり詳しくないのですが、バイオロジーとの相性も良く、創薬などでもグラフ理論は利用されているそうです。
上記にもありますが、交通渋滞の予想の論文などは商業的なモチベーションが強いように思います。
これらのように、実際にネットワーク・グラフ理論の枠組みをビジネスに落とし込んだ事例も増えてきており、アカデミックな興味に止まらない発展をしてきているようです。
(私も何らかの形で実際の業務に活かしたいなー。)
1.2.2 機械学習手法の発展
古くは「ケーニヒスベルクの橋の問題」から「4色問題」まで長年議論されている数学の一大トピックであるグラフ理論ですが、近年の機械学習手法の発展でアプローチするための裾野が広がって来ているように思います。
特に、
- 確率的勾配法による分散表現手法の獲得
- 畳み込みニューラルネットワークの発展
が、発展の大きな役割を果たしていると考えています。これら2点について頻繁にベースモデルとして議論されるモデルを第3章でご紹介しています。
1.3 本ブログで扱うこと・扱わないこと
1.3.1 扱うこと
- グラフの行列を用いた数学的手法(第2章)
- 隣接行列(2.2節)
- 次数行列(2.3節)
- ラプラシアン行列(2.4節)
- Link prediction(第3章)
- 機械学習手法(第4章)
- ノードの分散表現を得るための基本的手法
node2vec(4.2節) - ノードの畳み込みニューラルネットワーク(4.3節)
- ノードの分散表現を得るための基本的手法
1.3.2 扱わないこと
- 実装について
k-meansや ロジスティック回帰などの教科書的内容- 確率的勾配法
イントロの最後になりますが本記事では 理論をまとめるにとどめており、実装編はまた後日書きたいと考えております 。
また、私共も初学者であり、誤ったことも書いてしまっているかもしれません。その際はご指摘いただけると幸いです。
Table of Contents
2 グラフの行列を用いた数学的手法
ここでは、図形的なものであるグラフを数式として扱うための手法について簡単に紹介します。
2.1 扱うグラフの種類
グラフ \(G\) は集合の対 \( (V(G), E(G)) \) であり、 \(V(G)\) をグラフ \(G\) の点集合あるいは頂点集合(vertex set)、
\(E(G)\) を \(G\) の辺集合(edge set)と呼びます。
\(V(G)\) が空集合であることはありませんが、\(E(G)\) は空集合であっても良いため、グラフの最小単位は1つだけのノードになります(これを単点グラフと呼びます)。
今回の話では、 単純グラフ(simple graph) のみを扱うこととします。

Figure 2: 単純グラフの例
単純グラフは \(V(G)\) の元の数 \(|V(G)|\) が有限で、ループも多重エッジもないグラフのことです。

Figure 3: 【参考】単純グラフ以外の例
また、今回扱うグラフはエッジを持たないノードが存在しないことを仮定します。
このようなグラフを考えるため、ノード \(u,v \in V(G)\) をつなぐエッジ \(e \in E(G)\) を \(e = uv\) と表すことにします。
2.2 隣接行列
グラフは頂点集合 \(V(G)\) 、辺集合 \(E(G)\) で表されることを紹介しました。
この節ではグラフをより定量的に扱うための第一歩として 隣接行列(adjacency matrix) \(A(G)\) を導入します。
グラフ \(G\) の点集合が \(V(G) = \{u_1, u_2, \cdots , u_p\}\) であるときの隣接行列 \(A(G)\) を考えます。その成分を \(a_{ij}(i,j=1,\ldots,p)\) と表すと、隣接行列は、
\begin{align} a_{ij} = \begin{cases} 1 \quad u_iu_j\in E(G)\\ 0 \quad u_iu_j \not\in E(G) \end{cases} \end{align}で定義されます。
例えば図2の単純グラフで隣接行列 \(A\) を計算してみると、
となります。
隣接行列は、その名の通りノード \(u_i(i=1,\ldots,p)\) に隣接するノードがどれだけ存在するかを表しています。実際にそれが計算によって表されていることを見るために、ノード \(u_i\) を \(i\) 番目の成分のみが \(1\) 、その他の成分がすべて \(0\) である \(p\) 次元ベクトルで表してみます(このようなベクトルをone-hot vectorと呼ぶことにします)。
ノードを表現するone-hot vector \(u_i\) に隣接行列 \(A\) をかけると、\(u_i\) と隣接するノードがわかります。
そのことを先ほど求めた隣接行列を使って確かめてみましょう。\(u_3\) に隣接行列をかけてみると、
であり、グラフの図と一致していることが確かめられます。
また、隣接行列に対して次の定理が成り立つことが知られています。
\(V(G)=\{u_1,u_2,\cdots,u_p\}\) であるグラフ \(G\) の隣接行列を \(A(G)\) とする。このとき、隣接行列の \(n\) 乗 \(A^n(G) (n\geq 1)\) の \((i,j)\) 成分はグラフ \(G\) における長さ \(n\) の異なる \(u_i,u_j\) の経路の個数になる。
したがって、隣接行列を用いることで、隣り合うノード間だけでなく、グラフ全体の繋がりを表現することができると考えられます。
2.3 次数行列
グラフ \(G\) のノード \(u\) に接続するエッジの数を次数と呼び、 \(d(u)\) と表します。上の定理から、隣接行列の2乗 \(A^2\) の対角成分は \(d(u_i) (i=1,\ldots, p)\) であることがわかります。この対角成分のみを抜き出した行列、つまり行列の \((i,i)\) 成分にノード \(u_i\) の次数 \(d(u_i)\) を置いた対角行列 \(C\) を次数行列と呼びます。
\begin{align} C = \begin{pmatrix} d(u_1) & 0 & \cdots & 0\\ 0 & d(u_2) & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & d(u_p) \end{pmatrix} \end{align}2.4 ラプラシアン行列
ここまでに定義した隣接行列 \(A(G)\) と次数行列 \(C(G)\) を使って次の行列 \(L(G)\) を定義します。
\begin{align} L(G) \equiv C(G) - A(G) \end{align}この \(L(G)\) をラプラシアン行列(Laplacian matrix)、または単にラプラシアンと呼びます。ラプラシアン行列 \(L(G)\) は、グラフ \(G\) の情報を持たせた行列の一種であり、隣接行列同様、グラフを定量的に扱う上で重要な対象になります。
ラプラシアンという名前が付いていることでお気づきの方も多いと思いますが、2階微分作用素のラプラシアン \(\Delta = \nabla^2\) と類似の作用をする演算子になります。これらのつながりを説明する方法は色々とあるようですが、ここでは与えられたグラフ \(G\) に対して、勾配と発散をあわせた量が計算されているな、くらいの粒度の説明をします。
具体例として、先程利用した隣接行列からラプラシアン行列を求めてみると次の形になります。
\begin{align} L = \begin{pmatrix} 3 & -1 & 0 & 0 & 0 & 0 & -1 & -1\\ -1 & 3 & -1 & 0 & 0 & 0 & -1 & 0\\ 0 & -1 & 4 & -1 & -1 & 0 & -1 & 0\\ 0 & 0 & -1 & 2 & -1 & 0 & 0 & 0\\ 0 & 0 & -1 & -1 & 3 & -1 & 0 & 0\\ 0 & 0 & 0 & 0 & -1 & 1 & 0 & 0\\ -1 & -1 & -1 & 0 & 0 & 0 & 4 & -1\\ -1 & 0 & 0 & 0 & 0 & 0 & -1 & 2 \end{pmatrix} \end{align}では、今回も \(u_3\) にラプラシアン行列 \(L\) を作用させてみましょう。
\begin{align} L u_3 = - u_2 + 4u_3 - u_4 - u_5 - u_7 \end{align}右辺の \(u_3\) の係数は次数行列から来ている次数 \(d(u_3) = 4\) であり、ノード \(u_3\) に接続するエッジの数であった訳ですが、これはノード \(u_3\) から流出する量を表していると解釈できます。さらに、それが流れていく方向はどちらなのか、というと \(u_2, u_4, u_5, u_7\) に重み1ずつで流れていく、ということまでが上の式から分かります。すなわち、ラプラシアン行列をノードに対応するベクトルに作用させると、そのノードの発散と勾配と解釈できる量が計算できました。
ここの例では少し単純すぎたかもしれませんが、重み付き・向き付きのグラフでは、勾配の強さや流れの向きが表せることがおわかりになると思います。
非常に大雑把にではありますが、ラプラシアン行列 \(L\) がラプラシアン \(\Delta\) に対応する演算子であることを説明しました。ラプラシアン \(\Delta\) の固有ベクトル(固有関数)である指数関数が、方程式の解析で重要な枠割を果たしたように、ラプラシアン行列の固有ベクトルもグラフの性質を調べる上で重要になります。これについては具体的に4章のConvolutional Neural Network Graphで利用します。
以下ではラプラシアンの固有ベクトルを \(\chi_i\) 、固有値を \(\lambda_i\) と表すことにします。
3 Link Prediction
隣接していない2つのノードを考えたとき、この2つのノードは繋がり得るだろうか?
ということを考える問題をLink Predictionと呼びます。このような問題は、時間変化するようなグラフで考えられることが多いようです。例えば、Facebookで「知り合いかも」と出てくるユーザーは、自分とはつながっていませんが、繋がりそうなユーザーを予測しています。これはまさにLink Predictionが使われている例になります。
ノードの組 \(u,v\) に対し、ノードの繋がりやすさを測るスコアが考えられています。
- Common Neighbors : \(|N(u) \cap N(v)|\)
- Jaccard's Coefficient : \(|\frac{N(u) \cap N(v)}{N(u) \cup N(v)}|\)
- Adamic-Adar Score : \(\sum_{t\in N(u)\cap N(v)}\frac{1}{\log |N(v)|}\)
- Preferential Attachment : \(|N(u)|\cdot|N(v)|\)
ただし、\(N(u)\) はノード \(u\) に隣接するノードの集合をあらわします。例えばCommon Neighborsのスコアを考えると、共通する隣接ノードが多いほどスコアが高く、\((u,v)\) は繋がりやすいと考えられます。
上に挙げたスコアは、全てグラフ \(G\) が与えられたら( \(V(G),E(G)\) が定められたら)求めることが可能であり、そのようなスコアをこの記事ではヒューリスティックなスコアと呼ぶことにします。
3.1 Link Prediction と AUC
Link Predictionのスコアは様々なものが考えられていますが、対象とするグラフに対してそのスコアが良いスコアであるか測る指標として、AUCがよく利用されます。AUCを計算するために、次のように問題を設定しましょう。
グラフ \(G(V,E)\) が与えられたときに、 \(G\) のノード全てを繋いだグラフを考え、
そのグラフのエッジの集合を \(U\) と表します。このとき \(|U|=|V|(|V|-1)/2\) であり、 \(U-E\) はグラフ \(G\) には存在しないエッジの集合になります。
Link Prediction では、 \(U-E\) に含まれる(存在しない)エッジに対しスコアを計算し、
スコアの高いノードは繋がりそうだ、と考えます。ただし、存在しないエッジのスコアのみではスコアの良し悪しは測れないため、 \(E\) の中からランダムにエッジを選び、それらに対してもスコアを計算します。ランダムに選んだエッジの集合を \(E^P\) と表すと、 \(E^P\) に含まれるエッジのスコアは \(U-E\) に含まれるエッジのスコアよりも高いことが期待されます。
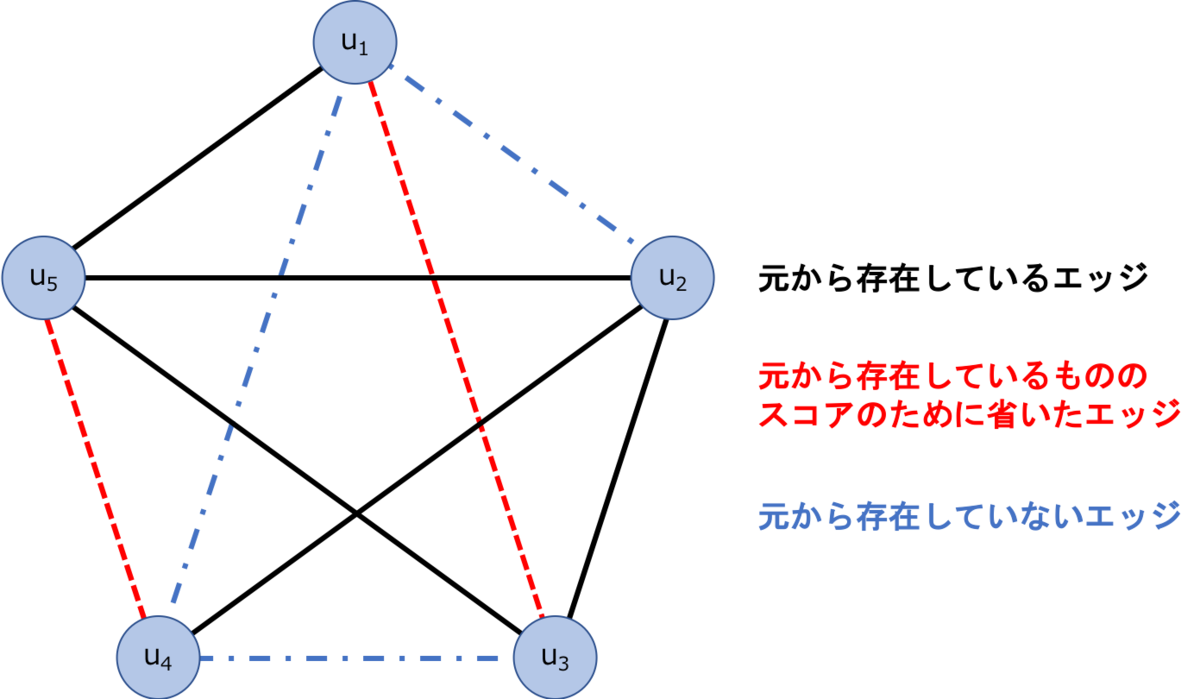
Figure 4: 破線のエッジに対してスコアを計算する。赤破線はテストのために取り除いた、本来は存在するエッジ。
それでは、具体例とともにAUCの計算をしていきたいと思います。
図4のグラフを考えます。ランダムに選ぶエッジとしてここでは(1,3), (4,5)を選びましょう。また、存在しないエッジは(1,2), (1,4), (3,4)になります。上で定義した集合の要素としては以下のとおりです。
\(E^P, U-E\) に含まれるエッジのスコアを計算する必要がありますが、今回はエッジ \((i,j)\) のスコア \(s_{ij}\) をCommon Neighborsで与えてみます。
\begin{align*} s_{12} = 1,\quad s_{13} = 1,\quad s_{14} = 0,\quad s_{34} = 1,\quad s_{45} = 1 \end{align*}\(E^P\) のスコアの方が \(U-E\) と比較して高いことが期待されるので、
きちんと高いスコアが出ていたのか、表を作ってみます。
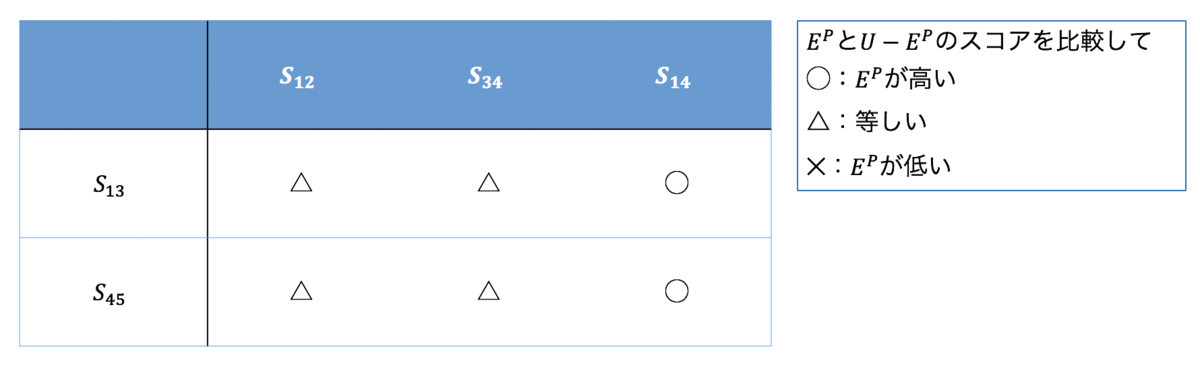
Figure 5: スコアを比較したときの"勝敗"表。理想的には全て勝っていると良い。
上の表をもとに以下の手順でROC曲線を描いてみます。
- 縦軸の \([0,1]\) 区間を \(E^P\) の要素の数で等分する。今の例では2等分する。
- さらに横軸の \([0,1]\) 区間を \(E-U\) の要素の数で等分する。今の例では3等分する。
- 3等分にした横軸の各区間を、\(U-E\) のエッジのスコアが高いものから順に担当させる。
- 各区間で担当しているスコアに対し、上記の表で勝ちならば1ブロック、引き分けならば1/2ブロックの面積を塗りつぶす。
- 塗りつぶした面積を囲う線がROC曲線となる。
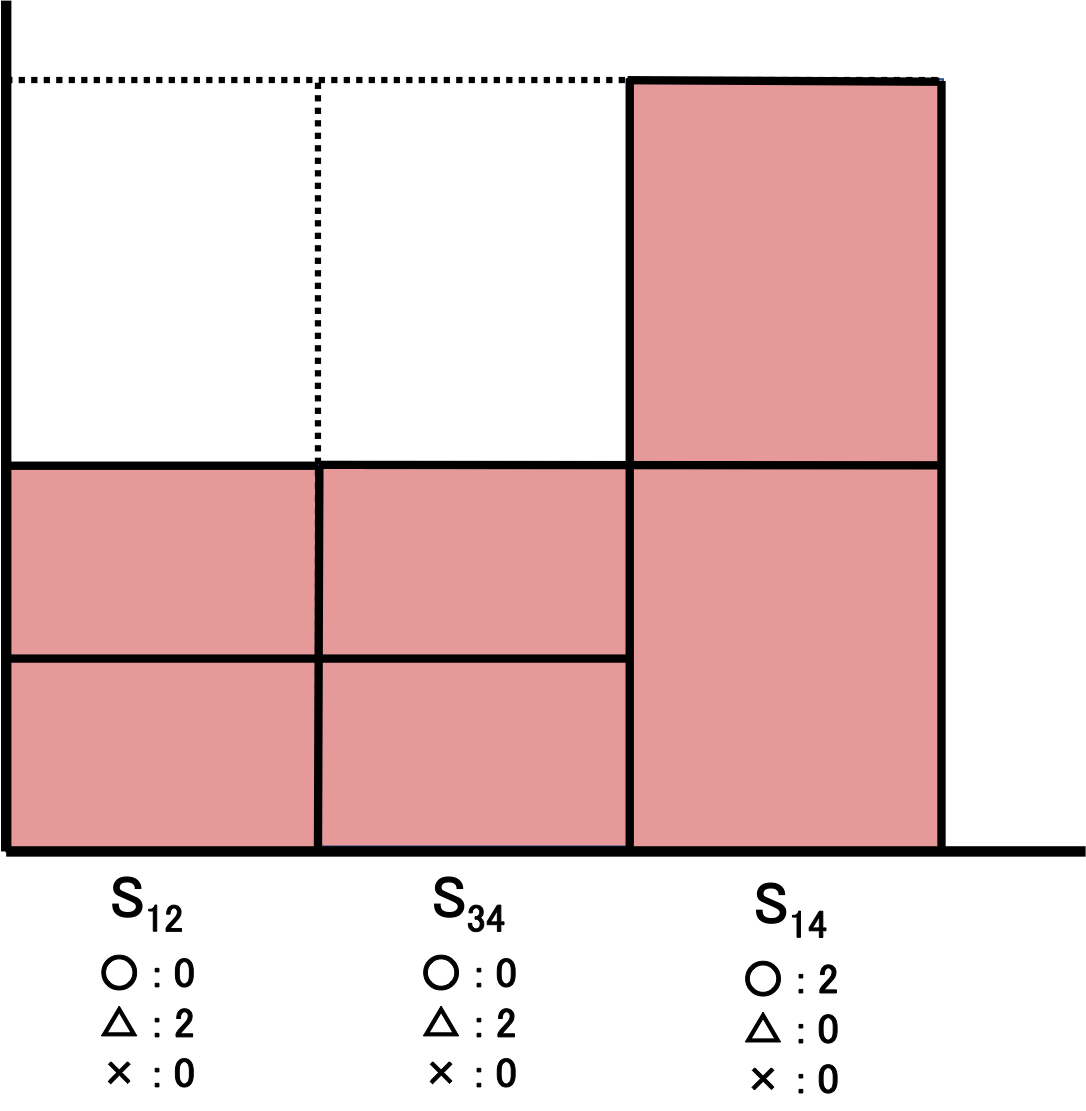
Figure 6: 対応するROC曲線
この手順に従って描いたROC曲線が上の図になります。
また、AUCは以下の公式によって与えられることもわかります。
ただし \(n\) は \(E^P, U-E\) のスコアの組み合わせの数 \(n=|E^P||U-E|\) 、 \(n'\) は \(E^P\) のスコアが \(U-E\) のスコアより高かった数、 \(n''\) はスコアが等しかった数になります。上記の表でAUCを計算してみると、
\begin{align} \mbox{AUC} = \frac{2 + 0.5\times 4}{6} = \frac{2}{3} \end{align}となります。
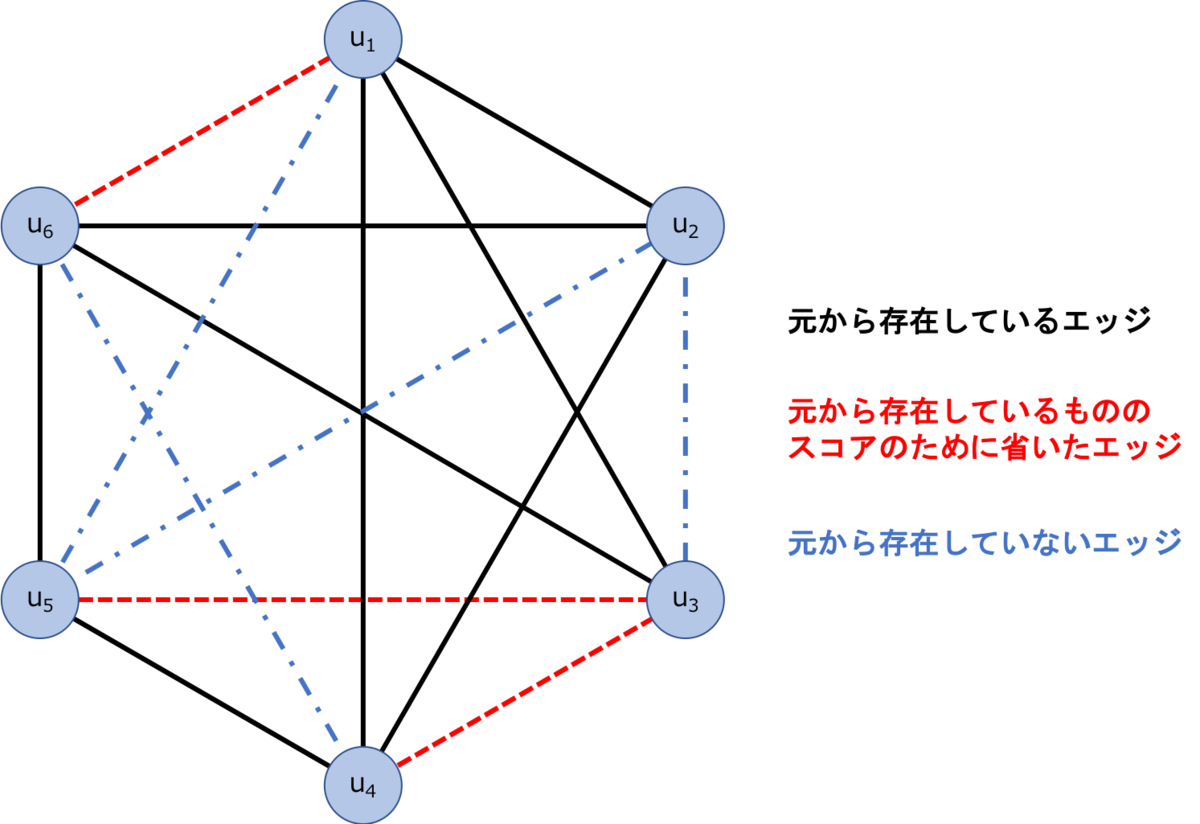
Figure 7: 1個だけノードを増やしてみる。
もう一つ別のグラフ(上図)を使ってAUCを計算してみます。 \(E^P, U-E\) はそれぞれ次の通りになります。
\begin{align} E^P &= \{(1,6), (3,4), (3,5)\}\\ U-E &= \{(1,5), (2,3), (2,5), (4,6)\} \end{align}前の例と同様に、Common Neighborsでスコアを計算します。
\begin{align*} s_{16}&=2,\quad s_{34}=1,\quad s_{35}=1,\\ s_{15}&=1,\quad s_{23}=2,\quad s_{25}=2,\quad s_{46}=2 \end{align*}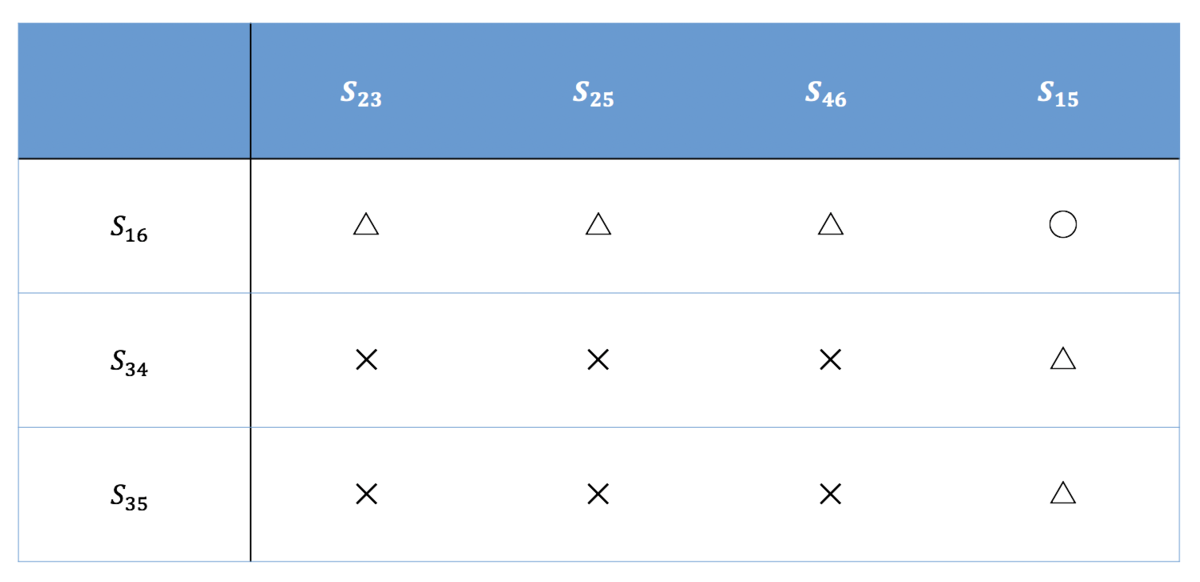
Figure 8: スコアの勝敗表
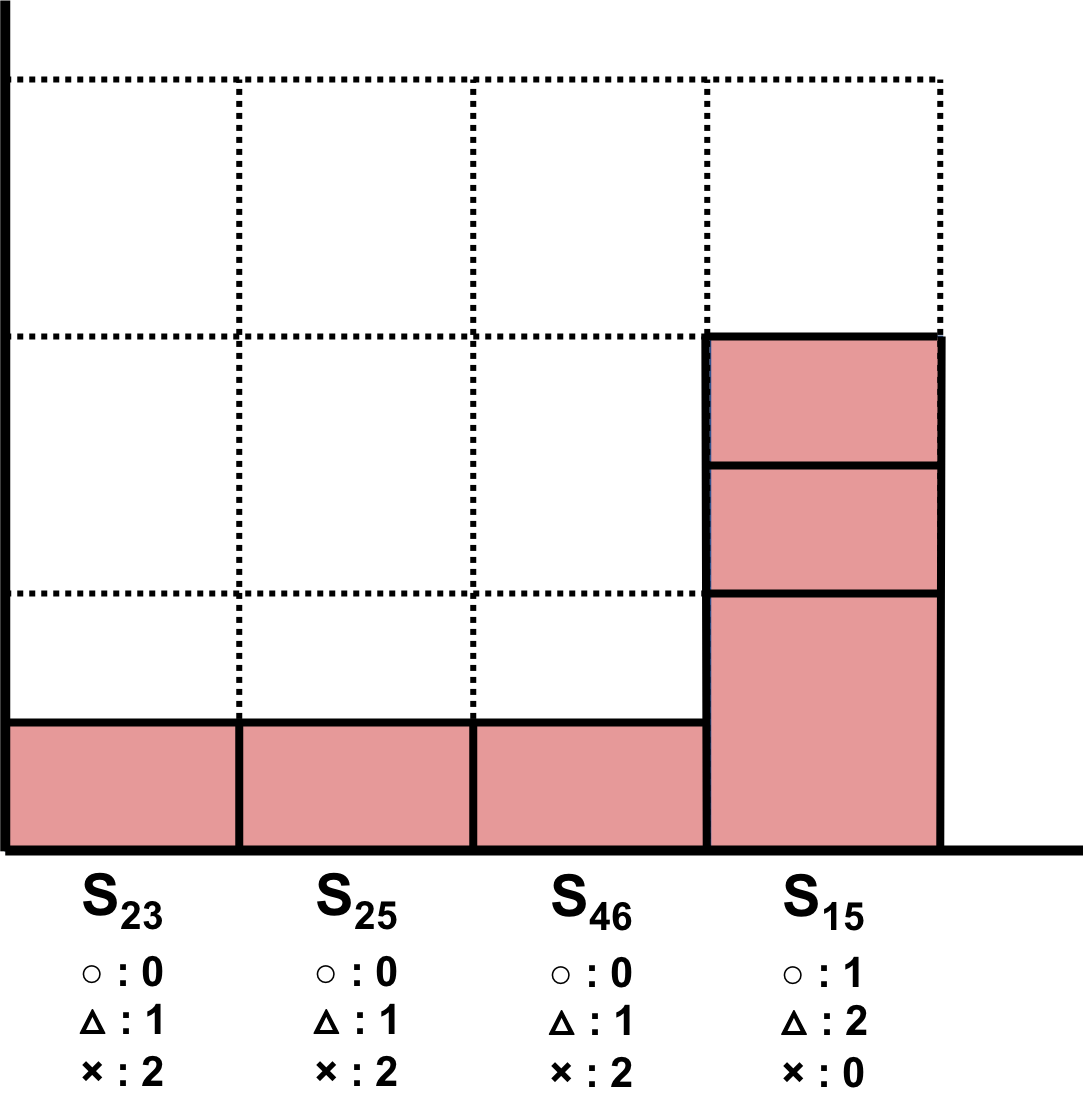
Figure 9: 図5のグラフでCommon Neighborsを利用したときのAUC
得られたスコアからROC曲線を描いたものが図7になります。AUCは、
\begin{align} \mbox{AUC} = \frac{1 + 0.5\times 5}{12} = \frac{3.5}{12} \end{align}となります。スコアの時点で明らかに分かるのですが、恐ろしく精度が悪いです。
このようにCommon Neighborsのように直感的に分かりやすいものでも、計算してみるとあまり精度がよくないこともあります。そのため、ヒューリスティックなものだけでも様々なスコアが存在します。
このあとの章では node2vec を利用してLink Predictionのスコアを計算する方法も紹介します。
4 グラフの機械学習的アプローチ
上記にもあるように、近年の機械学習手法の発展によって、グラフに対するアプローチの裾野が広がって来ているように思います。
一方グラフ理論のことを勉強する前はグラフ理論の話を聞いても、適応範囲はイメージしやすいものの一体何をインプットしていて、何をアウトプットしているのかがわからない程度には難しく感じました。勉強した今では過去の自分に「グラフ理論思っているよりも難しくない体系なんやで。」と伝える気持ちでまとめました。
本章では(おそらく)現在のスタンダードなグラフに対するアプローチの2手法「 node2vec 」と「グラフにおける畳み込みニューラルネット」を扱います。
タスクによって出力の形式は異なることはあるものの、ノードやエッジの 分散表現化 は重要な工程です。その グラフの分散表現の新しい取得方法 を提案しているのが node2vec です。
一方、グラフにおける畳み込みニューラルネットワークは 直接的にグラフアルゴリズムのタスクを予測するアーキテクチャ を組むことになります。具体的には「ノードの分類」と「Link Prediction」などが挙げられます。
4.1 入力データセットについて
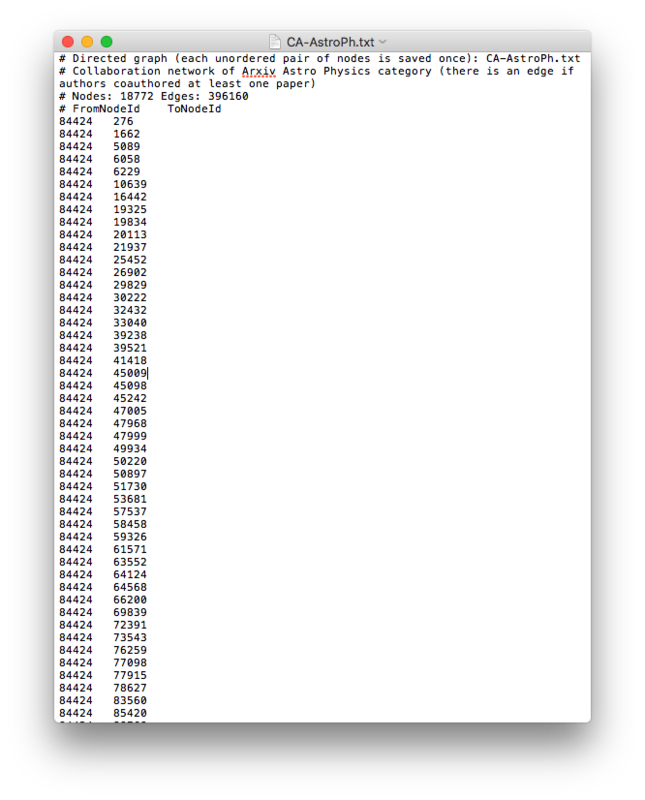
第2章で数学的なグラフの扱い方を説明してきました。隣接行列を用いることで基本的にはグラフ全体を表現することができます。ですが実際には、隣接行列はスパースな行列が多く、メモリを無駄に食いがちです。そこで共起するデータセットをインプットデータとして扱います。具体的には以下の図のような共起するIDを羅列したデータを入力します。
このデータはオープンアクセスな論文データベースであるarXivのAstro Physics(天文物理)における共著者を共起データとしてまとめられたものです。共著論文を書いたか書いてないかの2値になるはずなので、無向グラフでエッジに重みなどは付いていません。エッジに重みがある場合には3列目のカラムに重みが入ったデータセットになるはずです。このようなデータがモデルの入力データセットになります。
4.2 node2vec
node2vec の原論文[2, 3]を読んで自分なりの解釈も含め紹介して行きます。 node2vec のアルゴリズムを簡単にまとめると
- グラフからノードをサンプル
サンプルされたデータが文章のような時系列データとして扱われる - サンプルデータを元にノードの分散表現を得る
ノードのSkip-GramでNegative samplingをして、確率的勾配法から分散表現を得る
下記に node2vec で分散表現を得るまでの流れを図として表現しました。自然言語処理における単語の分散表現化を理解していれば、ノードのサンプリングにランダムウォークを使うだけなので、そこまで抵抗感を抱かないのではないでしょうか?

Figure 11: node2vec のアルゴリズム概要
論文では得られる分散表現に対する複数の実験を行なっており、それについても紹介いたします。
4.2.1 グラフからノードの時系列をサンプル
まず、グラフからノードをサンプリングする過程を紹介します。インプットデータからグラフ内の2ノードがリンクしているのか否かを判断することは可能です。ここから、リンクしているノードに下図のようなランダムウォークを繰り返して固定長(長さ \(l\) )のサンプルを用意します。ランダムウォークとは、次に移る位置を確率的に無作為に決定される運動過程のことを指します。

Figure 12: ランダムウォークとして赤いエッジを通ってノードがサンプルされたとする
ランダムウォークとしての確率分布を以下のように定義します。
\begin{align} P(c_i = u_a | c_{i-1} = u_b) = \begin{cases} \pi_{u_a u_b} / Z \qquad & \text{if}\ \ (u_a, u_b) \in E\\ 0 & \text{otherwise} \end{cases} \end{align}\(\pi_{u_a u_b}\) が \(c_i\) から \(c_{i-1}\) に遷移する確率、 \(Z\) が正規化定数を指します。ここではエッジのないノード間の確率が \(0\) となり、エッジのあるノード間に正規化されていない確率 \(\pi_{u_a u_b}\) を仮定しているだけです。
このランダムウォークを 2パラメータで制御してサンプリングをする のが node2vec の最大の特徴です。論文中では 2nd order random walkと呼んでいます(一般的な呼称なのか知りません)。
今、ランダムウォークが \(t\rightarrow v\) に移動した直後の状態だと仮定します(下図)。つまり、今は \(v\) にいます。ノード \(v\) の次にどのノードに遷移するのかを \(\pi_{u_a u_b} = \alpha_{pq}(t,x) \cdot w_{v,x}\) の確率過程としてとらえます。ここで \(w_{v,x}\) はノード \(v,x\) 間のエッジの重みを指し、入力データにエッジの重みが存在する場合に生じます。 \(\alpha_{pq}(t,x)\) は
\begin{align} \alpha_{pq}(t,x) = \begin{cases} 1/p \qquad & \text{if} \ \ d_{tx} = 0\\ 1 & \text{if} \ \ d_{tx} = 1\\ 1/q & \text{if} \ \ d_{tx} = 2 \end{cases} \end{align}で定義されます。 \(d_{tx}\) は次ステップ候補のノード(今の場合 \(x\) と \(t\))が現在のノード(今の場合 \(v\))の1 step前のノード(今の場合 \(t\))と最短距離でどれだけ離れているかを指します。原理的に \(d_{tx} = \{ 0, 1, 2 \}\) の3パターンしか存在しません。この3パターンごとにそれぞれの確率過程を仮定するのが2nd order random walkです。
例えば \(t\) から見て \(x_1\) は最短ステップが \(d_{tx} = 1\) であり、 \(\alpha = 1\) になります。 \(t\) から見て \(x_2, x_3\) は2ステップ必要になるので \(d_{tx} = 2\) であり、 \(\alpha = 1/q\) です。最後に \(t\) から見て \(t\) は0ステップで到達するので \(\alpha = 1/p\) とわかります。
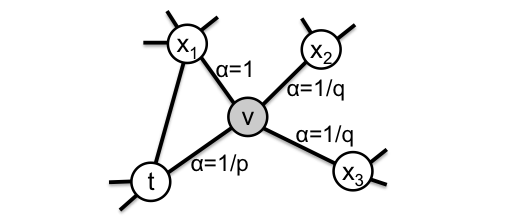
Figure 13: node2vec のランダムウォーク過程を説明する図。ノード \(t\) からノード \(v\) に移った段階で、次にノードに移る確率がどのような数値になるかを示している。
それぞれ
- p : Return parameter
- q : In-out parameter
と呼んでおり、文字通りの意味を指します。Return parameter \(p\) が大きい場合には、直前のノードに戻る確率は下がります。また、In-out parameter \(q\) が大きい場合にはより遠くのノードに遷移していく確率が下がります。それぞれどれくらいの値が大きいと言えるのかというと、比較対象は1です。むしろ、3パラメータで記述されるところを \(d_{tx} = 1\) の確率でオーバーオールに規格化していると理解しています。
サンプルする例を図にしました。今回の場合、 \(l=5\) でノード \(u_1\) からスタートするサンプルを図にしています。この \(u_1\) からスタートするランダムウォークを \(r\) 回繰り返します。

Figure 14: ランダムウォークによってサンプルされたノードを並べた図。 node2vec では \(l\) 個のノードを \(r\) 回、全ノードに対して思考する。
図では \(u_1\) からスタートしたサンプルしかありませんが、この作業を全ノードからサンプルします。
後にも登場しますが、 DeepWalk と呼ばれる手法では \(p=q=1\) でエッジのあるノードに等確率で遷移するサンプリングをする手法になります。
4.2.2 単語の分散表現を得るのと同様(Skip-Gram)に分散表現を得る
単語の分散表現を得る word2vec では分散表現空間内で前後の単語を予測しています。 word2vec に手法自体はC-BoWもありますが node2vec ではSkip-Gramを採用しています。( word2vec についての参考ページ )。
node2vec では2nd order random walkでサンプルした時系列に対して対象ノードの前方k個のノードを予測します。下図では前方3ノード( \(k=3\) )で色を塗りました。
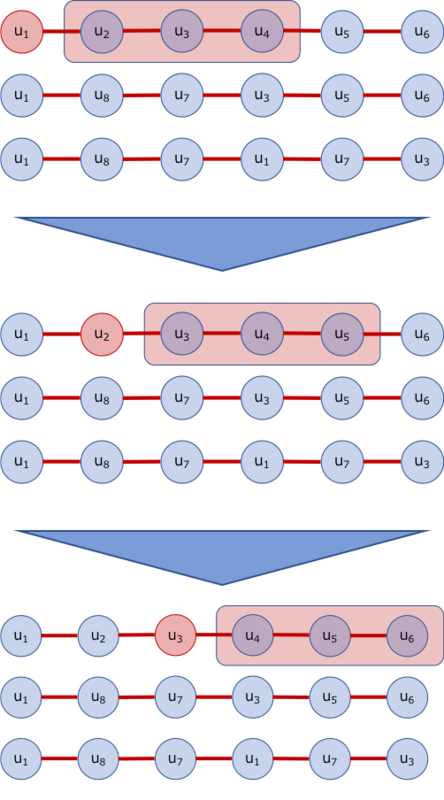
Figure 15: 赤いノードから赤の領域のノードを予測する。 node2vec では対象のノードの前方 \(k\) 個のウィンドウ幅を予測する。
赤のノードを表現する分散表現から、赤背景のノードの分散表現を予測するように全ノードについて最適化を行います。ノード \(u_i\) から得られる \(d\) 次元分散表現を \(f(u_i)\) と書くと
\begin{align} \max_f \sum_{u\in V} \log Pr(N_S(u)|f(u)) \end{align}上記の確率を最大化するように分散表現への変換行列 \(f\) を更新することになります。ここで \(N_S(u)\) は一般にはノード \(u\) 周りの近傍ノードを指しますが、今回の場合上記で説明した対象点より \(k\) 個幅のノードを指します。
ここで以下の仮定をします。
- 同時確率 → 近傍ノード同士の独立性
- 内積 → 分散表現空間内の2ノードの対称性
上記の仮定から \(Pr(N_S(u)|f(u))\) は近傍ノード \(N_S(u)\) の同時確率に置き換えることができ、
\begin{align} Pr(N_S(u)|f(u)) = \prod_{n_i\in N_S(u)} Pr(n_i|f(u)) \end{align}そして、この確率に分散表現空間内の対称性を仮定しsoftmax関数として捉えます。
\begin{align} Pr(n_i|f(u)) = \frac{\exp\left[f(n_i)\cdot f(u)\right]}{\sum_{v\in V}\exp\left[f(v)\cdot f(u)\right]} \end{align}`` \(\cdot\) ''は分散表現間の内積を指します。上記の過程から式(5)は
\begin{align} \max_f \sum_{u\in V} \left[-\sum_{n_i\in N_S(u)}\log Z_u + \sum_{n_i\in N_S(u)}f(n_i)\cdot f(u) \right] \end{align}と変形できます。ここで \(Z_u = \sum_{v\in V} \exp(f(v)\cdot f(u))\) の分配関数である。この \(Z_u\) は実際にはnegative samplingなどを使って計算コストを減らさないと全ノードに対する演算が基本的には終わらないでしょう。
これを解くように確率的勾配法を行うことになりますが、著者らのコードを見ると、 gensim の word2vec をそのまま使っています。これによってサンプリングの部分しか書く必要がなくなり、空行も含めても250行程度で書かれています。
4.2.3 algorithm
ここまでのコードをまとめたものが下になります。

Figure 16: node2vec のアルゴリズム
4.2.4 Experiments
まず、探索方法として Breadth-first Sampling(BFS) と Depth-first Sampling(DFS) の二種類が存在します。

Figure 17: BFSとDFSの違い。
- Breadth-first Sampling(BFS)
- 近傍を探索する
- 近傍の点との関係性をより詳細に学習することができ、ノード間のハブや橋渡し、孤立ノードなど各々の役割同士似たノードが近い特徴になる
- このような構造上の役割に重きを置かれた同一性を structural equivalence と呼んでいる
node2vecの場合\(p\) が大きく \(q\) が1か小さめな値に対応する
- Depth-first Sampling(DFS)
- 深さ優先で探索する
- 深さ優先のため、大域的な理解が分散表現に反映される
- 各々のサンプルでグラフ全体を広く学習するため、近傍ノード間が近い特徴を持つ
- homophily equivalence と呼ばれる特徴
node2vecの場合\(p\) が小さく \(q\) は大きな値に対応する
上記の2つのサンプリング方法は \(p, q\) を調節することで実現されます。サンプリング方法ごとに得られるノードの分散表現は当然異なるものになります。人間が求める目的ごとに上記の2つは使い分けられるべき存在となります。
- サンプリング方法の違い(レ・ミゼラブルの登場人物)
レ・ミゼラブルの登場人物(ノード)が同時に登場する回数(エッジ)を重み付きのグラフとして分散表現に変換します。データ自体は
- 77 nodes
- 254 edges
です。このネットワークを \(d = 16\) 次元の分散表現空間に登場人物を埋め込みます。さらに、作られたノードの分散表現を
k-meansでクラスタリングし、そのクラスごとに色を塗った図が下記になります。
Figure 18: レ・ミゼラブルの登場人物の共起ネットワークを
node2vecで学習させたもの。 \(p,q\) の数値の違いからBFSとDFSの違いが起こり、分散表現の数値が異なってくる。上図が \(p=1, q=0.5\) で学習させた分散表現をk-meansでクラス分けした図。下図が \(p=1, q=2\) で学習させクラス分けした図。前節で紹介したように上の図(DFS)では近傍ノードが同一クラスタと判別され、下の図(BFS)では構造的に同一なノードが同一クラスタと判断されました。目的に応じて異なるパラメータにし、異なる分散表現に埋め込むことになります。
- Multi-label classification
ノードの分散表現からあらかじめ付与されている正解ラベルを予測します。分散表現をクラス分けするタスクに使うに耐えうるかを実験したものという解釈です。
- 比較モデル
- Spectral Clustering
DeepWalk
- \(p = q = 1\) の
node2vec
- \(p = q = 1\) の
LINE
- 1stepの近傍点と2stepの近傍点の予測で別々の目的関数を作り分散表現を得て、それぞれの分散表現をconcatする
DeepWalkは \(p, q\) のパラメータを無くした純粋なランダムウォークになり、node2vecに比べモデルの自由度は低いものになります。したがって、以後の実験でもDeepWalkがnode2vecの精度を上回ることはありません。
LINEは対象のノードから同心円状に2step分のノードの予測から分散表現を得たものです。先にネタバレをしてしまいますが、以下の実験では固定幅のステップしか探索しない分node2vecやDeepWalkに精度で劣ってしまう結果になってしまっています。 - Spectral Clustering
- データセット
- BlogCatalog
- ブロガーがノード、友達関係をエッジとしたネットワーク
- ブロガーがどんな分野に興味を持っているかをラベルとして持っているデータ(登録時にあらかじめ決められているカテゴリらしい)
- データ量
- 10,312 nodes
- 333,983 edges
- 39 different labels
- Protein-Protein Interactions (PPI)
- PPIのwikipediaページ
- (著者の知識が足りず、調べても何のデータなのか明確に良く分かりませんでした。)
- データ量
- 3,890 nodes
- 76,584 edges
- 50 different labels
- Wikipedia
BlogCatalogでは近い興味を持った人同士が友達になりやすいhomophily equivalenceが予想できます。ですが、イメージしてもらえば分かると思うのですが、アカウントの存在を知っているが友達にはなっていない「Familiar Strangers」と呼ばれる人たちもおり、これがstructural equivalenceな特徴を持っていると論文著者らは予想しています。
PPIは申し訳ありませんが、調べても既に生物や化学の背景知識のある人への解説しか見当たらず、私には理解できませんでした。しかし、structuralとhomophilyな特徴を両方持っていると予想しています。 - BlogCatalog
- 実験結果
全てのモデルで \(d =129\) 次元に埋め込んでいます。
node2vecとDeepWalkはそれぞれ \(r = 10,\ l = 80\ k = 10\) で学習しています。node2vecでは \(p,q \in \{0.25,0.50,1,2,4\}\) のグリッドサーチをした結果をスコアとしています。
得られた分散表現をロジスティック回帰(w/ L2正則化)の分類を行い、正しく分類されたかをMacro-F1で評価した値を下表に記しています。
Figure 19: 各々のグラフデータを
node2vecを用いて分散表現化し、全体のラベル付けされたノードの50%を用いて学習させラベル予測させた結果。数値は Macro-F1で評価した値を指す。下から2行目が
node2vecの最高精度を出した \(p,q\) のセットであり、node2vec以外の最高精度に対して何%精度が向上したかが最後の行に表されています。当然、パラメータの自由度の分だけDeepWalkには勝る結果になります。またLINEよりは良い結果を得られています。また、上のデータごとの論文著者らの予想は結構外れています。例えば、BlogCatalogではベストなセッティングとして \(p=0.25, q=0.25\) と低く、structuralとhomophillyな特徴を同様に持っている結果になりました。PPIに関してはベストなセッティングとして \(p=4, q = 1\) とhomophilyな特徴に見えますが、 \(p=q=1\) の
DeepWalkとそこまでスコアに変化がなく、 \(p\) の依存性よりランダムウォークでの探索が非常に重要であると結論づけています。さらに、同様のデータセット・同様に得られた分散表現を用いてロジスティック回帰での学習データセット数を変化させて実験をさせています。以下の図が結果で横軸がtrainデータの割合です。

Figure 20: ラベルのついた学習データの量の変化に伴う性能評価。 \(x\) 軸がデータセットの何割を使って学習したかを指し、 \(y\) 軸が評価値を指す。
Spectral Clusteringや
LINEよりDeepWalkとnode2vec少ないデータで精度が良い結果を出す事ができています。また、データセットの量や性質ごとに使い分ける際の目安になるのではないかと思っています。
- 比較モデル
- Parameter sensityvity & Perturbation Analysis
パラメータに
node2vecがどれだけ影響されるのかを示したのが以下の図(a)です。BlogCatalogのデータを使ってデフォルトnode2vecのパラメータを使っています。 \(p, q\) はデフォルトでは \(1\) です。
特徴としては \(p, q\) は小さい方が精度が上がるようです。ベストなセッティング( \(p = q = 0.25\) )に近くなると同時に、グラフ自体の特徴なので「そうなのかー」という印象です。
\(d\) は増加共に精度も上がります。が、表現力が上がっているので当然の結果です。100次元くらいからサチるようです。
同様に \(r, l\) も増加共に精度も向上しますが、サンプルの量が増えるのでこれも当然の結果だと考えています。
サンプルのウィンドウ幅 \(d\) も増加と共に精度も向上する傾向にあるようです。自然言語処理での単語の分散表現でもウィンドウ幅を幾つにするのかは議論の余地があるので、ここは何とも言えません。
Figure 21: (a):パラメータ依存性、(b):BlogCatalogネットワークでのエッジの欠損やノイズの影響
上の図の(b)はノード間ののエッジを抜いたり増やしたりした場合、精度にどのように影響するかを実験した結果です。実際の世界では完全な状態のグラフが得られているとは限りません。グラフネットワークの論文をいくつかみても、ダイナミカルに時間発展するグラフを扱う論文を多く見ます。このように熱平衡状態に至っていないグラフを扱うのは非常に重要な調査です。
結果はそこまで精度が下がらなかったものの、ノイズとしてエッジが増えてしまう実験の方が精度の減衰が急だったことが分かりました。 - Scalability
グラフは非常に多くのノードとエッジの情報を扱う必要があり、計算時間が非常にかかってしまうことが課題の一つになっています。
node2vecでの学習時間のスケールの仕方を実験した結果になります。
Erdős-Renyi graphと呼ばれるグラフを使ってグラフの大きさを増やして行ったときの学習終了までの時間を評価する実験です。(Erdős numberで有名なErdősさんとRenyiさんが体系を作った、ランダム・ネットワークと呼ばれるものです。ここの文脈ではBlogCatalogなどの特定のグラフは有限なのに対してErdős-Renyi graphは無限に増やすことができるという理解以上は必要ないと思います。将来、Erdős-Renyi graphやその拡張のWatts Strogatz modelについても本ブログで扱っていきたいと考えています。)
主に時間がかかってしまうのはノードをサンプルする工程です(小さいネットワークの場合、逆転します)。この効率的なサンプリング方法はDeepWalkの時に考案されており、Alias samplingと呼ばれるものらしいです(調べていないっす。。。)node2vecではこれを採用しているらしいです。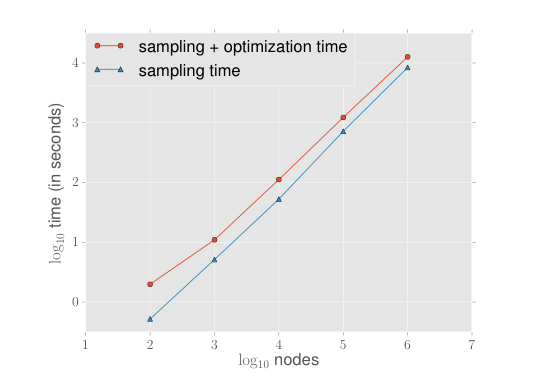
Figure 22: 学習時間のノードの数依存性。Erdős-Renyiグラフを使っている。
- Link prediction
2つのノード間にエッジが存在するのかを予想します。2章では古典的なLink predictionの方法を取り扱いました。Link predictionはFacebookの「友達かも?」やamazonの「あなたにオススメ」など現在繋がっていない人や商品を繋がせるレコメンドができるため、非常に商業的に実用的なタスクになります。(真偽のほどは知りませんが)分散表現の特徴量を使ったLink predictionはこれまで行われてこなかったそうです。
実験のセットアップを説明します。- ネットワークからランダムに50%のエッジを取り除く(2つのグラフに分割されないように注意)
- 取り除かれたエッジは接続している正例としてのデータセットとして保持しておく(つまり2ノードのペアと、その正解というラベル)
- 正例を取り除く前の時点で繋がっていない2つのノードをランダムに正例数と同数取ってくる(2ノードのペアと、その不正解というラベル)
これでデータセットの完成です。正例としてエッジを取り除いたグラフでノードの分散表現を取得します。獲得した分散表現を用いてTable 1の演算を作成したデータセットのペアにしたノード間に行います。
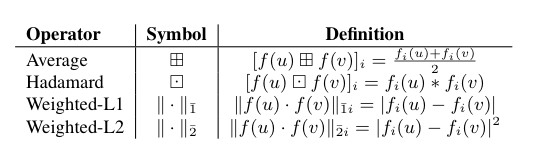
Figure 23: エッジの特徴を学習するための様々な二項演算子の表。
Table 1の演算では同じ次元のベクトルが得られます。この2ノード間から得られたベクトルを分類器の入力にし、正解/不正解ラベルを当てるように予測します。ちなみに論文には学習器や学習パラメータが載っていません。Multi-label classificationでロジスティック回帰を使っているので おそらく これで分類します。もちろん学習にはtrainとtestに分けて評価したのでしょう。そのAUCを評価指標として他のモデルと比較します。その結果がTable 4の(a)~(d)になります。2章で紹介したAUCでの結果が表の1段目にスコアを載せています。

Figure 24: 上表がヒューリスティックなカウントベースのリンク予測。 \(\mathcal{N}(u)\) はノード \(u\) の近接ノードを指す。下表がそれぞれのデータセットに対するリンク予測のAUCスコアを記した表。その際のノード間の二項演算子は(a)Average,(b)Hadamard,(c)Weighted-L1,(d)Weighted-L2を指す(Figure 14に定義)
評価に使ったデータセットは以下の通りです。
- Facebook
- 友人関係のネットワーク
- データ量
- 4,039 nodes
- 88,234 edges
- PPI
- 「Multi-label classification」の章と同様
- データ量
- 19,708 nodes
- 390,633 edges
- arXiv ASTRO-PH
基本的に比較モデルより
node2vecは上回る精度を発揮しました。特に、2ノード間の分散表現の演算はアダマール積を取ると精度が良いようです。一方、ベクトルの平均化では精度が上がらないようです。
4.3 畳み込みニューラルネットを用いたGraph Convolution
グラフ理論では、畳み込みニューラルネットを用いた機械学習的アプローチが近年非常に盛んに発表されてきているように感じます。そもそも、主に画像処理などで用いられる畳み込みニューラルネットは、基本的に規則的にノードが並んでいないグラフなどを学習するのには困難があります。ここで紹介するConvolutional Neural Network Graph(CNN-GRAPH)とRelational Graph Convolutional Networks(R-GCNs)はベースモデルとして多く引用される論文の手法です。本章では、これら2手法がどのようにして畳み込みニューラルネットに落とし込むのかを簡単に紹介します。
またアーキテクチャとして今回は畳み込むところまでの数理について説明します。タスクごと何に最適化するかによって出力形式を定め、最適化する損失関数やアーキテクチャを追加して学習させてください。
4.3.1 Convolutional Neural Network Graph(CNN-GRAPH)
おそらく共通の呼称がないようなのでCNN-GRAPHと呼ぶことにします[4]。原論文となるのは Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering と Deep Learning on Graphs: A Survey です。
CNN-GRAPHでは2章で登場したグラフラプラシアンを用いて畳み込みを行います。そのために必要になってくるフーリエ変換と畳み込み積分も踏まえ説明します。
- グラフフーリエ変換
一般的なフーリエ変換のアナロジーとして、グラフのフーリエ変換が存在し グラフフーリエ変換(Graph Fourier Transform) と呼ばれています。この対応関係の理解のために、一般的なフーリエ変換から説明して行きます。
一般的な、フーリエ変換は以下のように定義される変換のことを指します。
\begin{align} F(k)=\mathcal{F}[f(x)]= \int^\infty_{-\infty} f(x) e^{-ikx} dx \end{align}ここで \(i\) は虚数を指します。上記の右辺では、関数 \(f(x)\) と関数 \(\exp(-ikx)\) の内積をしており、フーリエ変換は「互いに直交する基底関数として指数関数を用いて、 基底関数を重み \(f(x)\) で足し合わせること 」を意味するのだと理解しています。また、コンピュータサイエンスの枠組みでは離散的な処理しかできないため基本的に離散フーリエ変換を扱うのですが、今回は著者が理解しやすいように連続関数を使用しています。
\begin{align} f(x) = \mathcal{F}^{-1} [F(k)] = \frac{1}{2\pi} \int^\infty_{-\infty} F(k) e^{ikx} dk \end{align}
また、フーリエ変換の性質として逆変換が存在し次のように計算されます。このアナロジーとして、グラフフーリエ変換が定義されています。具体的にはラプラシアン行列の固有ベクトル \(\chi_i\) を用いてグラフ上の信号 \(x \in R^{|V|}\) (基本的にはグラフ中の1つのノードを指すベクトルと考えて差し支えありません)のグラフフーリエ変換を
\begin{align} \mathcal{F}[x] = U^T x \quad \in R^{|V|} \end{align}として定義します。ここで、 \(U = [\chi_0, \chi_1, \cdots , \chi_{|V|-1}]\) は \(L\) の対角化行列です( \(L = U \Lambda U^T,\ \Lambda = {\rm diag}(\lambda_0, \lambda_1, \cdots, \lambda_{|V|-1})\) )。一般的なフーリエ変換で互いに直交する基底関数として指数関数を用いたのに対して、グラフフーリエ変換では互いに直交するラプラシアン行列の固有ベクトルを用いて固有ベクトル空間に信号を射影します。この対応関係からグラフフーリエ変換と呼ばれています。
\begin{align} x = U \mathcal{F}[x] = U U^T x \end{align}
また、ラプラシアン行列 \(L\) が実対称行列ですので \(U\) は直交行列となり、逆グラフフーリエ変換はとして逆変換が記述できます。
- 畳み込み積分
前節では「グラフフーリエ変換の定義」と「フーリエ変換とグラフフーリエ変換の対応関係」を紹介しました。基本的にフーリエ変換特有の性質はグラフフーリエ変換でも適応できます。本節では関数の畳み込み積分(Convolution、合成積)について説明し、フーリエ変換の畳み込み積分とそれに対応するグラフフーリエ変換の畳み込みについて紹介します。
\begin{align} (f\ast g)(x) = \int^\infty_{-\infty}dy f(y)g(x-y) \end{align}
一般的な関数の畳み込み積分は以下のように定義されます。畳み込み積分を指す二項演算子を \(\ast\) で記しています。上記の畳み込み積分のフーリエ変換で畳み込み定理と呼ばれるものが定まります。
\begin{align} \mathcal{F}[f\ast g] &= \mathcal{F}\left[\int^\infty_{-\infty} dy f(y)g(x-y)\right] \nonumber\\ &= \int^\infty_{-\infty}dx \int^\infty_{-\infty}dy f(y)g(x-y) e^{-ikx} \nonumber\\ &= \int^\infty_{-\infty}dy f(y) \int^\infty_{-\infty}dx g(x-y) e^{-ikx} \nonumber\\ &= \int^\infty_{-\infty}dy f(y) \int^\infty_{-\infty}dt g(t) e^{-ik(t + y)} \nonumber\\ &= \int^\infty_{-\infty}dy f(y) e^{-iky} \int^\infty_{-\infty}dt g(t) e^{-ikt} \nonumber\\ &= \mathcal{F}[f] \mathcal{F}[g] \end{align}ここで最終行の積は関数をベクトルとみなした場合、アダマール積(要素積)となっています。また、両辺で逆フーリエ変換をすることで畳み込み積分がフーリエ変換を使って、
\begin{align} (f\ast g) = \mathcal{F}^{-1} [\mathcal{F}[f] \mathcal{F}[g]] \end{align}と記述できます。ここまでをグラフフーリエ変換に適応すると、
\begin{align} x \ast_G y &= \mathcal{F}^{-1} \mathcal{F}[x] \mathcal{F}[y] \nonumber\\ &= U\left\{ (U^Tx) \odot (U^Ty) \right\} \nonumber\\ &= U\left\{ \rm{diag} (U^Tx) (U^Ty) \right\} \end{align}\(\ast_G\) はグラフでの畳み込み演算を指します。ここで \(f_\theta \in R^{|V|}\) をフィルターとして \(\Theta \equiv \rm{diag} (U^T f_\theta)\) とすると
\begin{align} x \ast_G f_\theta = f_\theta \ast_G x = U\Theta U^T x \end{align}これでグラフ上に定義された信号 \(x\) のフィルター \(f_\theta\) による畳み込み積分を定めることができました。
この畳み込み演算を多層に重ねて、フィルタのパラメータを更新することでディープなラーニングができます。実際にはCNN同様、複数のフィルターを使用することで畳み込みます。第 \(l\) 層には \(f_l\) チャネルの入力がありそれと同数のフィルターを用意し、それぞれ各フィルタを通した成分を足し合わせて活性化関数 \(\rho\) に入れ、その出力を次の第 \(l+1\) 層目に渡します。
\begin{align} x_j^{l+1} = \rho \left( \sum_{i=1}^{f_l} U \Theta_{i,j}^l U^T x_i^l \right), \quad j = 1,\cdots ,f_{l+1} \end{align}ここで \(i,j\) は用意する個々のフィルタ(チャネル)を指し、第 \(l+1\) 層目ではフィルタ(チャネル)の数を \(f_{l+1}\) 個想定した式になります。信号 \(x\) はベクトルであるものの、添字 \(i\) はベクトルの成分を指すわけではないことに注意してください。 \(x_i^l\) は第 \(l\) 層目の \(i\) 番目のチャネルのベクトルを指します。CNNと似ているものの、部分的にフィルタをかけるわけではなく一つのフィルタでグラフ全体に作用させる点で一般的なCNNとは異なる構造をしています。この畳み込みニューラルネットがCNN-GRAPHになります。
- CNN-GRAPHの長所と短所
4.3.2 Relational Graph Convolutional Networks(R-GCNs)
原論文は Modeling Relational Data with Graph Convolutional Networks です。R-GCNsと呼ばれており、先ほどのCNN-GRAPHに比べ直感的に比較的理解しやすい構造をしています。そのためか他解説記事も多く存在します。またR-GCNsの特徴として、有向グラフやループを含むループグラフ、多重グラフなどにも適応できるモデルになります。
先に図でアーキテクチャがどのような構造をしているのかを理解し、続いて数式での説明をしていきます。

Figure 26: R-GCNsの概念図
上記の図がR-GCNsの原論文から取ってきたものになります。 rel_r がノードの属性を指す条件を指し、 rel_r の条件を満たす隣接ノードを畳み込み足し合わせます。例えば、各ノード周りに隣接する全ノード、ソーシャルネットワークなどでは隣接ノード中の女性のノードや、隣接ノード中のフォロワーの数が10未満のノードなどがそれぞれの rel_r の条件になります。有向グラフでは rel_r の内、「対象のノードに向かっているか?(in)」「対象ノードから外に向かっているか?(out)」を別々の特徴量としてカウントします。例えば上図だと、対象のノード(赤)に条件 rel_1 で関係し合う隣接ノード(青)が4つ入ってくる向きを持っています。出ていく向きを持った隣接ノードは2つです。一方、 rel_N 下の隣接ノードは in = 1 で out = 3 になっており、それらのノードをまとめて畳み込む操作をしています。最後にある self-loopは自身に戻るループエッジを指します。それらをモデルの入力値として非線形な活性化関数を通して対象のノードの畳み込み層となります。
続いて上記の描像を数式として解釈します。畳み込みの定義式は以下になります。
\begin{align} x^{l+1}_i = \rho \left( \sum_{r\in\mathcal{R}} \sum_{j\in\mathcal{N}^r(i)} \frac{1}{c_{i,r}} W_r^l x_j^l + W_0^l x_i^l \right) \end{align}ここで、 \(\mathcal{R}\) は考慮する関係として \(\mathcal{R} = \{ rel\_1, \cdots, rel\_N \}\) を指し、 \(\mathcal{N^r(i)}\) が \(r\) の属性に含まれる第 \(i\) ノードの隣接ノードを指します。 \(x_j^l\in R^{d^l}\) は第 \(l\) 層目の第 \(j\) ノードのベクトルを指し、 \(W_r^l\) が第 \(l\) 層目の関係 \(r\) 専用の重みを指します。 \(W_0^l\) は上図にもあるようにループに対する重みを指し、 \(\rho\) は活性化関数を指し ReLU などを使用します。また、 \(c_{i,r}\) は異なる関係を同じスケールに落とし込むための規格化定数であり \(c_{i,r} = |\mathcal{N}_i^r|\) などを使用します。
上記の式では1ステップ近傍のみのノード情報を畳み込むことになりますが、2層3層と層を重ねるごとに対象ノードの2,3ステップ先の情報が引き継がれることになります。
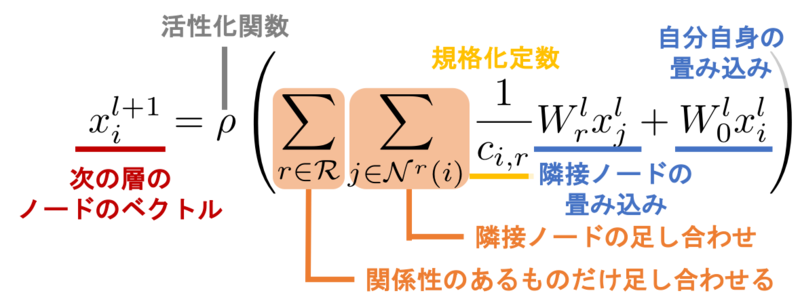
しかし上記の定式化では、各レイヤーごと関係性ごとに重みを用意するため非常に多くのパラメータが使われます。本事項は、多くの関係性を持ったグラフデータでは すぐに過学習状態に至ってしまうという問題 があります。R-GCNsの解説記事をいくつか読みましたが、この問題と解決法について省いてまとめられていました。個人的にはこのモデルでグラフを学習する上ではこの操作が必須であり、非常に重要な操作なのだと考えています。論文ではこの問題に対してblock-diagonal-decompositionとbasis-decompositionの2つの正則化でのアプローチが提案されています。
-
block-diagonal-decomposition
\begin{align} W^l_r = \bigoplus_{b=1}^B Q_{br}^l \end{align}上式で \(B\) はハイパーパラメータとなり、多いほど全パラメータ数は少なくなります。 \(W^l_r\) はブロック対角な行列 \({\rm diag}(Q_{1r}^l, \cdots, Q_{Br}^l)\) となります。行列 \(Q_{rb}^l\) 以外の零成分の分だけパラメータが落とされており、過学習を防げます。
-
basis-decomposition
\begin{align} W^l_r = \sum_{b=1}^B a_{rb}^l V_b^l \end{align}上式では \(a_{rb}^l\) はスカラー量、 \(V_b^l\in R^{d^{(l+1)}\times d^l}\) で \(W^l_r\) と同じ次元になります。こちらはblock-diagonal-decompositionとは異なり、 \(B\) が少ないほど全パラメータ数は少なくなります。またbasis-decompositionの特徴として、 \(r\) に依るパラメータはスカラー量 \(a_{rb}^l\) のみであり \(V_b^l\) は \(r\) に依らず共通の行列が使用されます。
上式からもわかるように、block-diagonal-decompositionでは重み行列に rel_r のスパースな制限を重み行列に課しています。これはノードが密接に関係し合っている何かしらのグループが存在していて、グループ間では重みを共有するものの、グループを横断的に関係はしないだろうという直感を反映しています。一方、basis-decompositionでは rel_r に対し重みの共有をしているので rel_r そのものの重要度を反映されます。
ここまでの操作でグラフの畳み込みのための理解を終えます。上記でもお伝えした通り、誤差の更新や損失関数の最小化、実験結果などは本記事では扱いません。
5 おわりに
グラフ理論の勉強したこと、調べたことを長々と本ブログにてまとめてみました。
- グラフの行列を用いた数学的手法
- 隣接行列
- 次数行列
- ラプラシアン行列
- Link prediction
- グラフの機械学習的アプローチ
- グラフの分散表現化
node2vec
- 畳み込みニューラルネット
- Convolutional Neural Network Graph
- Relational Graph Convolutional Networks
- グラフの分散表現化
内容は上記になります。著者二人とも以下の2点からグラフ理論に手をつけました。
- 数学的な面白さ・興味があったこと
- ビジネス応用のしやすそうな技術なのではと思ったこと
軽い気持ちでまとめようと本ブログを初めてみましたが、思ったよりもはるかに細かいところが気になってしまい長い文章になってしまいました。しかし、グラフ理論の体系は非常に広く、現在も勉強中です。私共も現在読んでいるのですが、「ネットワーク科学: ひと・もの・ことの関係性をデータから解き明かす新しいアプローチ」などは読んでいて非常に面白いです。ただ500ページ近くあり大型本で非常に質量があるのが難点です。もっと短くグラフ理論の内容を理解するのには「グラフ理論序論」もおすすめです。
ビジネスとの関わりも強い分野であるのは確信があるので、何らかの形で仕事に活かしたいっすねー。
今後もグラフ理論だけでなく、各々の興味に基づきブログを更新していきたいと思っております(あ、宿題の実装編もやりますよ)。我々の感性に則った文章をつらつらと書いていきますが、マインド等に共感を感じていただけるのであれば今後も読んでいただけると幸いです。改めてですが、私共も初学者であり誤ったことも書いてしまっているかもしれません。その際はご指摘いただけると幸いです。また、いいねやシェアしていただけると書く気力に繋がるのでポチってください。
6 参考文献
- graph-based-deep-learning-literature/conference-publications (github)
機械学習関連の有名国際会議に採択された graph関連論文 がまとめられています -
node2vec: Scalable Feature Learning for Networks
Aditya Grover and Jure Leskovec
Stanford UniversityarXiv:1607.00653
3 Jul 2016
ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), 2016 -
node2vec著者のサイト - 原論文著者のコードが
cnn_graphという名前でした。(github) -
Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering
Michaël Defferrard, Xavier Bresson and Pierre Vandergheynst
EPFLarXiv:1606.09375
30 Jun 2016
Neural Information Processing Systems (NIPS), 2016. -
Deep Learning on Graphs: A Survey
Ziwei Zhang, Peng Cui and Wenwu Zhu
Tsinghua UniversityarXiv:1812.04202
11 Dec 2018 -
Modeling Relational Data with Graph Convolutional Networks
Michael Schlichtkrulla, Thomas N. Kipfa, Peter Bloemb, Rianne van den Berga, Ivan Titova and Max Wellingc
a. University of Amsterdam
b. VU Amsterdam
c. University of Amsterdam, CIFARarXiv:1703.06103
17 Mar 2017