Pseudo Theory of Everything

データサイエンス初心者物理学徒の奮闘記

トップ > 正則化 > わしの思うリッジ回帰(L2正則化)と正則化法。

わしの思うリッジ回帰(L2正則化)と正則化法。

正則化 機械学習 数学 スパースモデリング

 

1 はじめに

最近、我々+数名でスパースモデリングという分野を勉強しています。詳細はまた別の記事にて紹介するにして、今回はスパースモデリングの前段階に当たる リッジ回帰(ridge regresion) に脚光を当てます1。
読者には釈迦に説法かもしれませんが、リッジ回帰は L2 正則化とも呼ばれ機械学習の中でも非常にスタンダードな概念の一つになっています。しかし専門的に正則化法を扱ってみて、案外知らなかったことを知れたのでまとめました。
まず、リッジ回帰での損失関数は以下のような式で記述されます。

\begin{align} E = (y - X \vec{w})^2 + \alpha \vec{w}^T \vec{w} \end{align}

上記の損失を最小化するように係数の重みベクトル \(\vec{w}\) を推定します。解析的には \(\vec{w}\) について微分をしたものが \(0\) となる係数の重みベクトルを見つける最適化問題です。通常の正則化法を用いない回帰の場合は \(\alpha = 0\) の損失を考えることになります。通常の回帰問題から見ると、右辺の第2項は罰則項と呼ばれる項にあたります。上記の最適化問題の結果、

\begin{align} \vec{\hat{w}} = (X^T X + \alpha I)^{-1} X^T \vec{y} \end{align}

がリッジ回帰の解として得られます。ここまでは多くの技術ブログや本に載っています。しかし、「過学習が防げるようになります」等の大義名分のもと、「やってみた」になるわけですが、「いやいや、何で罰則項入れただけで過学習が抑えられるん?そもそも何で罰則項にこの形で重み自身を追加されるん?」って思っていました。

本編ではそれにお答えしましょう。以下のことが分かるようになります。

  • リッジ回帰の罰則項は、なぜあの形で導入されるのか
  • 汎化性能を上げるためとの理解があるが、それは本当なのか
  • 何で 正則化法 と呼ばれるのか

上記の事柄を理解するために下記について順を追って説明していきます。

  1. 線形回帰モデルのおさらい
  2. リッジ回帰の自然な導出
  3. 正則化たる所以

「線形回帰モデルは流石に知っているよ!!」という方は次章にて一般的なことしか書かれていないので、飛ばしてもらっても問題ないと思います。ぜひ「リッジ回帰くらい知っているよ!!」という方にも、線形回帰モデルの章以降は読んでもらいたいです。ググってもあまり出てこないし、しっかり理解している方はそこまで多く無いのではないかと思っています。
(「正則化法」でググって最初のページに出てくるようになりたいなー……。)

 

2 線形回帰モデルのおさらい

 

2.1 理論編

いま、データ \(\mathcal{D}\) として \(N\) 個の \((\vec{x}, y)\) の観測値のペア

\begin{align} \mathcal{D} = \{(\vec{x}_1, y_1),(\vec{x}_2, y_2),\ldots, (\vec{x}_N, y_N)\} \end{align}

があるとします。このとき \(\vec{x} \in R^D\) から \(y\) を予測するモデルは回帰モデルと呼ばれます。特に \(D \geq 2\) 次元の入力値から正解データ \(y\) を予測することは 重回帰(multiple regression) と呼ばれています。具体的には重み係数 \(\omega_0, \omega_1,\ldots,\omega_D\) を用いて、

\begin{align} \hat{y} &= \omega_0 + \omega_1 x_1 + \omega_2 x_2 + \cdots + \omega_D x_D\nonumber\\ &= \vec{w}^T \vec{x} \end{align}

で正解データ \(y\) を予測することを指します。ここで \(\vec{w}^T = (\omega_0, \omega_1, \ldots, \omega_D),\ \vec{x}^T = (1, x_1, \ldots, x_D)\) であり、内積で簡潔に書くことができます。
\(N\) 個のデータについて並べると

\begin{align} \begin{pmatrix} \hat{y}_1 \\ \hat{y}_2 \\ \vdots \\ \hat{y}_N \end{pmatrix} = \begin{pmatrix} \vec{w}^T \vec{x}_1 \\ \vec{w}^T \vec{x}_2 \\ \vdots \\ \vec{w}^T \vec{x}_N \end{pmatrix} = \begin{pmatrix} \vec{x}_1^T \\ \vec{x}_2^T \\ \vdots \\ \vec{x}_N^T \end{pmatrix} \vec{w} \end{align}

上記で注意すべきは下付き添字はデータのラベルを指すものであり、ベクトルの成分とは別のものであることと、各々の \(\vec{x}\) の成分に等しく重みベクトル成分がかかることです。ここで最後の等式に現れた \(\vec{x}^T\) を縦に並べたものを \((D + 1)\times N\) の行列として下記のように見ることができます。

\begin{align} \begin{pmatrix} \hat{y}_1 \\ \hat{y}_2 \\ \vdots \\ \hat{y}_N \end{pmatrix} = \begin{pmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1D}\\ 1 & x_{21} & x_{22} & \cdots & x_{2D}\\ \vdots & \vdots & \vdots & & \vdots\\ 1 & x_{N1} & x_{N2} & \cdots & x_{ND}\\ \end{pmatrix} \begin{pmatrix} \vec{\omega}_0 \\ \vec{\omega}_1 \\ \vec{\omega}_2 \\ \vdots \\ \vec{\omega}_D \end{pmatrix} \end{align}

上記の \(x_{ij}\) と \(1\) で構成された行列 \(X\) を 計画行列(design matrix) と言います。
結果、計画行列と重み係数ベクトル \(\vec{w}\) を用いて

\begin{align} \vec{\hat{y}} = X \vec{w} \end{align}

と簡単に書くことができます。 \(\vec{\hat{y}}\) は \(X, \vec{w}\) で予測される出力値の列になります。

この予測値を正解データに近づけるために、最適化する誤差式を定義します。

\begin{align} E &= \sum_{i=1}^N (y_i - \hat{y}_i)^2 = \sum_{i=1}^N (y_i - \vec{w}^T \vec{x}_i)^2 \nonumber\\ &= (\vec{y} - X \vec{w})^T (\vec{y} - X \vec{w}) \end{align}

いわゆる二乗誤差であり、この誤差関数を最小化することは最小二乗法と呼ばれます。

誤差関数 \(E\) を \(\vec{w}\) に対して最小化するためには \(\vec{w}\) で微分し、 \(0\) になる \(\vec{\hat{w}}\) が \(E\) を最小化する係数の重みベクトルとなります。ここでは導出を省きますが、

\begin{align} \vec{\hat{w}} = (X^T X)^{-1} X^T \vec{y} \end{align}

となります。

ここまでは推定のために仮定している関数が一次線形でした。より一般化すると

\begin{align} \begin{pmatrix} \hat{y}_1 \\ \hat{y}_2 \\ \vdots \\ \hat{y}_N \end{pmatrix} = \begin{pmatrix} 1 & \phi_1(x_1) & \cdots & \phi_H(x_1)\\ 1 & \phi_1(x_2) & & \phi_H(x_2)\\ \vdots & \vdots & & \vdots\\ 1 & \phi_1(x_N) & \cdots & \phi_H(x_N)\\ \end{pmatrix} \begin{pmatrix} \vec{\omega}_0 \\ \vec{\omega}_1 \\ \vdots \\ \vec{\omega}_H \end{pmatrix} \end{align}

と各々の関数 \(\phi_i\) を仮定し、各関数にそれぞれの重みをかけて出力を予測します。結果、計画行列と重み係数ベクトル \(\vec{w}\) を用いて

\begin{align} \vec{\hat{y}} = \Phi \vec{w} \end{align}

と簡潔に書くことができます。一次線形の回帰モデルの場合と同様、係数の重みベクトルは

\begin{align} \vec{\hat{w}} = (\Phi^T \Phi)^{-1} \Phi^T \vec{y} \end{align}

と推定できます。

2.2 実装編

真の関数形の周りに正規分布させた擬似データを作成します。真の関数は

\begin{align} y &= \omega_0 + \omega_1 x + \omega_2 x^2 + \omega_3 \sin(x)\\ \vec{w}^T &= (0.12,\ 0.23,\ 0.34,\ 4.32) \end{align}

とし、その周りに分散 \sigma^2 = 1.5 でデータを作成します。ここでの数値や関数は全て完全にその場の思いつきです。

from math import sin

from numpy import array
from numpy.random import normal
from numpy.random import rand


# -5から5の間に一様分布からxを200個生成する
x = 10. * rand(200) - 5.
# ノイズを正規分布(平均0, 標準分散1.5)として生成
def epsilon(): return normal(loc=0., scale=1.5.)

# 真の関数形 + ノイズ
def y(x, omega): return omega[0] + omega[1] * x + omega[2] * x*x + omega[3] * sin(x) + epsilon()

# 擬似データ生成!!
omega = array([0.12, 0.23, 0.34, 4.32])
data_set = array([y(i, omega) for i in x])

ここで通常回帰問題を解く場合、真の関数形は知り得ないため、たくさん関数を用意して計画行列を構築します。今回は \(x\) の0次から10次までを線型結合した

\begin{align} \hat{y} = \omega_0 x^0 + \omega_1 x^1 + \omega_2 x^2 + \ldots + \omega_{10} x^{10} \end{align}

を仮定します。この計画行列を元に \(\vec{\hat{\omega}}\) を予測し、プロット用のデータを生成し、プロットします。

import matplotlib.pyplot as plt
from numpy import dot
from numpy import linspace
from numpy.linalg import inv


# 計画行列を作成する
# 先に計画行列の行(row)を返す関数を作成し、計画行列(design_matrix)を作る関数を作成する
def row(x): return array([1, x, x**2, x**3, x**4, x**5, x**6, x**7, x**8, x**9, x**10])
def design_matrix(x, row): return array([row(i) for i in x])

# 計画行列生成!!
X = design_matrix(x, row)
# X^T X
X_sq = dot(X.T, X)

# 推定された係数の重みベクトル
omega_hat = dot(dot(inv(X_sq), X.T), data_set)

# 真の関数(F)と推定される関数(F_hat)
def F(x, omega): return omega[0] + omega[1] * x + omega[2] * x*x + omega[3] * sin(x)
def F_hat(x, omega): return omega[0] + omega[1] * x + omega[2] * x**2 + omega[3] * x**3 + omega[4] * x**4 + omega[5] * x**5 + omega[6] * x**6 + omega[7] * x**7 + omega[8] * x**8 + omega[9] * x**9 + omega[10] * x**10

# 真の関数と、推定された係数の重みベクトルから予測した数値
x_plot = linspace(-5.1, 5.1, 100)
y_plot = array([F(i, omega) for i in x_plot])
y_plot_hat = array([F_hat(i, omega_hat) for i in x_plot])

# プロット
plt.xlim([-5.1, 5.1])
plt.ylim([min(data_set) - 2, max(data_set) + 2])
plt.grid(True)
plt.scatter(x, data_set, marker='x', alpha=0.8)
plt.plot(x_plot, y_plot, linewidth=3.5, color='gray')
plt.plot(x_plot, y_plot_hat, linewidth=3.5, color='orange')
plt.xlabel("x")
plt.ylabel("y")
plt.show()

下記が図示した結果になります。

f:id:pseudo-theory-of-everything:20191006163013p:plain

Figure 1: 200点の擬似データから予測される回帰線。灰色の実線が真の関数、オレンジ色の実線が回帰線。

生成されたデータを散布図で、灰色の実線が真の関数、オレンジの実線が最適化した関数になります。無事、真の関数に近い曲線がフィットできたと思います。

しかし、「 \(x^{10}\) まで高次の項まで考えて、過学習しないのか?」と多くの人は思うと思います。図を見れば分かりますがこの区間・上記のデータ数では十分フィットできます。

データ数を \(200\rightarrow10 + 2\) まで減らしてみます3。結果は以下の図のようになります。

f:id:pseudo-theory-of-everything:20191006162954p:plain

Figure 2: 少量データでの回帰線。灰色の実線が真の関数、オレンジ色の実線が回帰線。

あぁ、よく見る過学習の図になりましたね。こういう場合に有効なのが次章から紹介します 正則化法 になります。

3 リッジ回帰の自然な導出

第1章にも挙げましたが、

に本章では答えを与えます。

3.1 理論編

\(x\) が与えられたときの \(y\) の平均は線形回帰

\begin{align} \vec{w}^T \vec{x} \end{align}

であり、これにノイズ \(\epsilon\) が乗ったものとみなしたモデルを仮定します。つまり

\begin{align} y = \vec{w}^T \vec{x} + \epsilon, \qquad p( \epsilon ) = \mathcal{N} (0, \sigma^2) \end{align}

となります。注意したいのが、回帰線の周りに正規分布を仮定していますが、求めるのは最もデータセット \(\mathcal{D}\) を生成しやすいパラメータ \(\vec{w}\) を求めることになります(いわゆる最尤法です。また、 \sigma を推定しても良いのですが、今回は自由なパラメータとしています)。
ここで正規分布は

\begin{align} \mathcal{N}(x | \mu, \sigma^2) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left( - \frac{(x - \mu)^2}{2 \sigma^2} \right) \end{align}

です。
上記のノイズが乗ったモデルでは下記のように \(y\) の平均が \(\vec{w}^T \vec{x}\) で、分散が \sigma^2 のガウス分布に従っていることになります。

\begin{align} p(y) = \mathcal{N} (y|\vec{w}^T \vec{x}, \sigma^2) =\frac{1}{\sqrt{2 \pi} \sigma} \exp \left( -\frac{(y-\vec{w}^T \vec{x})^2}{2 \sigma^2} \right) \end{align}

再び \(\mathcal{D} = \{(\vec{x}_1, y_1),(\vec{x}_2, y_2),\ldots, (\vec{x}_N, y_N)\}\) を考えます。 \(\mathcal{D}\) の \(N\) 個のペア \((\vec{x}_n, y_n)\) が互いに独立であるとすれば

\begin{align} p(\vec{y} | X) = \prod^N_{n=1} p(y_n | \vec{x}_n)= \prod^N_{n=1} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left( -\frac{(y_n - \vec{w}^T \vec{x}_n)^2}{2 \sigma^2} \right) \end{align}

となります。この確率を最大化するパラメータを求めるのが最尤法であり、両辺に \(\log\) をとり、

\begin{align} \log p(\vec{y} | X) = - \frac{N}{2} \log (2 \pi \sigma^2) - \sum^N_{n=1} \frac{(y_n - \vec{w}^T \vec{x}_n)^2}{2 \sigma^2} \end{align}

が得られます。今、変動しうるのは \(\vec{w}\) であり、右辺第1項は定数と見なせます。また、 \(\log p(\vec{y} | X)\) を最大化することは、 \(-\log p(\vec{y} | X)\) の最小化と等価です。つまり、 \(\vec{w}\) に関して

\begin{align} -\log p(\vec{y} | X) = \sum^N_{n=1} (y_n - \vec{w}^T \vec{x}_n)^2 + (\mbox{定数}) \end{align}

を最小化する問題におきかえることができます。上記の式を見てわかるように、これが最小二乗誤差と一致しており、 正規分布をノイズとして考えた確率モデルと二乗誤差による線形回帰が等価 になっていることがわかります。

やっとこすっとこ正規化法に入ります。これまでに見てきたように、上記の式(22)ではデータ点に過学習してしまいます。そこで、尤度関数に正則化項を導入し過学習状態を防ぎます。ここで正則化法を用いるということは過学習を防ぐことを指すと考えます。過学習な状態とは \(\vec{w}\) の各成分 \(\omega_i\) の絶対値が極端にバラバラと大きく振れてデータ点に強くフィットしてしまう状態のことです。この状態を防ぐのですから、 \(\omega_i\) がそれぞれ独立に平均 \(0\) 、分散 \(\lambda^2\) の正規分布に従う確率変数であることを採用します。このような正規分布のパラメータの中で回帰問題を解くのですから、 \(\lambda\) が大きくなりすぎないよう制限をしてフィットし過ぎない状態を作り上げることができます。
数式を使ってここでの状態を表現していきたいとおもいます。 \(D+1\) 次元の係数の重みベクトル \(\vec{w}\) の確率分布を

\begin{align} p(\vec{w}) = \prod^D_{i=0} \mathcal{N}(\omega_i | 0, \lambda^2) \end{align}

と仮定します。この係数の重みベクトル \(\vec{w}\) の対数をとると、

\begin{align} \log p(\vec{w}) &= \sum^D_{i=0} \log \mathcal{N} (\omega_i | 0, \lambda^2)\nonumber\\ &= \sum^D_{i=0} \log \left( \frac{1}{\sqrt{2\pi\lambda^2}} \exp\left( - \frac{\omega_i^2}{2\lambda^2} \right) \right) \nonumber\\ &= \sum^D_{i=0} \frac{1}{2} \log \left( \frac{1}{2\pi\lambda^2} \right) + \sum^D_{i=0} \log \exp \left( - \frac{\omega_i^2}{2\lambda^2} \right) \nonumber\\ &= - \frac{D+1}{2} \log \left( 2\pi\lambda^2 \right) - \frac{1}{2\lambda^2} \sum^D_{i=0} \omega_i^2 \end{align}

になります。回帰の問題ではデータ \((X)\) から予測するのは \(\vec{y},\ \vec{w}\) を予測することになります。つまり \(p(\vec{y},\ \vec{w}|X)\) の最大化問題です。また \(\vec{y}\) と \(\vec{w}\) の同時確率分布は \(p(\vec{y},\ \vec{w}|X) = p(\vec{y}|\vec{w},\ X)p(\vec{w}|X) = p(\vec{y}|\vec{w},\ X)p(\vec{w})\) とかけます。

\begin{align} \log p(\vec{y}, \vec{w} | X) = \log p(\vec{y}|\vec{w}, X) + \log p(\vec{w}) = - \frac{N}{2} \log(2 \pi \sigma^2) - \frac{1}{2 \sigma^2} \sum^N_{n=1} (y_n - \vec{w}^T \vec{x}_n)^2 - \frac{D + 1}{2} \log(2 \pi \lambda^2) - \frac{1}{2 \lambda^2} \sum^D_{i=0} \omega^2_i \end{align}

整理して定数項を除き、最小化問題にするため両辺に負符号をかけてあげると

\begin{align} \frac{1}{\sigma^2} \sum^N_{n=1} (y_n - \vec{w}^T \vec{x}_n)^2 + \frac{1}{\lambda^2} \sum^D_{i=0} \omega_i^2 \propto (\vec{y} - X \vec{w})^2 + \alpha \vec{w}^T \vec{w} \qquad (\alpha \equiv \frac{\sigma^2}{\lambda^2} ) \end{align}

本記事の最初のリッジ回帰の式に一致しました。このように、リッジ回帰の正則化項は最小二乗法と同様に自然に導出された帰結であるのです。
式展開を追うことでお分かりだと思いますが、リッジ回帰の回帰係数 \(\alpha\) は実は

\begin{align} \alpha = \frac{\mbox{観測ノイズの分散}}{\mbox{重みベクトルの分散}} \end{align}

の比で表されます。つまり、 \(\alpha\) が大きい値をとる時には「観測ノイズの分散に対して重みベクトルの分散が小さい状態」を指すのでノイズのばらつきに対して関数がフィットしすぎないので過学習な状態を防げます( 大きすぎると重みベクトルの分散がない状態に近づくため、仮定するモデル(計画行列)を反映しないモデルになってしまいます )。逆に \(\alpha\) が小さい値をとる時には「観測ノイズの分散に対して重みベクトルの分散が大きい状態」を指すのでノイズのばらつきに対して関数がフィットしすぎてしまう過学習な状態になる可能性があります( \(\alpha = 0\) は第2章の帰結と等しく、過学習な状態を作ります )。
つまり、 \(\alpha\) の値は、 学習データのフィットについて観測ノイズと重み係数のどちらを重視するのかのバランスを決めるパラメータ ということがわかると思います。

3.2 実装編

では、リッジ回帰を用いて先ほどの過学習状態が緩和されたのか実践してみます。

from numpy import eye
# 正則化パラメータと正則化した重みベクトルを作る
alpha = 1.
omega_hat_re = dot(dot(inv(X_sq + alpha * eye(11)), X.T), data_set)

y_plot_hat_re = array([F_hat(i, omega_hat_re) for i in x_plot])

# プロット
plt.xlim([-5.1, 5.1])
plt.ylim([min(data_set) - 2, max(data_set) + 2])
plt.grid(True)
plt.scatter(x, data_set, marker='x', alpha=0.8)
plt.plot(x_plot, y_plot, linewidth=3.5, color='gray')
plt.plot(x_plot, y_plot_hat, linewidth=3.5, color='orange')
plt.plot(x_plot, y_plot_hat_re, linewidth=3.5, color='cyan')
plt.xlabel("x")
plt.ylabel("y")
plt.show()

コード中でありますが、正則化パラメータ \(\alpha = 1.0\) に取りました。上記のコードでプロットしたものが以下の図になります。

f:id:pseudo-theory-of-everything:20191006162934p:plain

Figure 3: リッジ回帰を用いた場合の回帰線。灰色の実線が真の関数、オレンジ色の実線がリッジ回帰を用いていない回帰線、シアン色の実線がリッジ回帰を用いた回帰線。

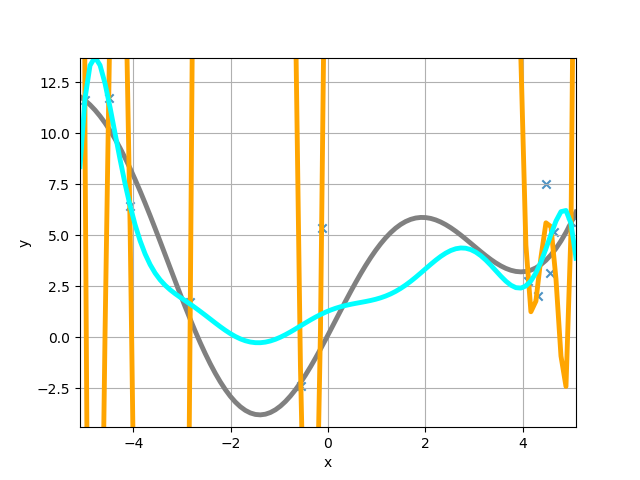
無事、過学習が緩和されたことがわかると思います。

最後に、理論編で重みベクトルを抑えるため分散という形でモデルを制限しました。それが実現しているかを確認しました。まず、正則化項を導入していない過学習状態の重みベクトルは

\begin{align} \vec{\hat{w}}^T = (36.907, 304.217, 438.961, -15.474, -97.963, -2.228, 8.010, 0.182, -0.286, -0.004, 0.004) \end{align}

となりました。最大 \(438.961\) 、最小 \(-97.963\) と非常に大きな分散を持っていることがわかります。これが過学習状態です。一方、正則化項を導入した重みベクトルは

\begin{align} \vec{\hat{w}}_{\rm reg}^T = (1.287, 0.989, -0.643, -0.0420, 0.331, -0.0004, -0.0435, -0.00040, 0.00226, 0.00002, -0.00004) \end{align}

となりました。最大 \(1.287\) 、最小 \(-0.643\) と実際に分散が小さくなったことがわかります。
正則化パラメータを \(\alpha = 1.0\) に置きましたが、データ点とシアン色の線との分散( \sigma )と重みベクトルの分散( \(\lambda\) )が同じ程度の大きさになっていることがわかります。

4 正則化たる所以

先にこの章の主張を伝えます。正則化法は2次の計画行列を 正則行列にする 操作のため正則化法と呼ばれます。これまで同様、理論編・実装編でみていきましょう。

4.1 理論編

まず、リッジ回帰での正則化項を導入した場合、推定される重みベクトルは

\begin{align} \vec{\hat{w}} = (X^T X + \alpha I)^{-1} X^T \vec{y} \end{align}

となります。上記の式の正則化の効果がない極限( \(\alpha = 0\) )では

\begin{align} \vec{\hat{w}} = (X^T X)^{-1} X^T \vec{y} \end{align}

になりますが、 \(X^T X\) が正則行列でない場合には逆行列が存在しないため、解を求めることができません。この状況を一歩踏み込んでみましょう。 \(X^T X\) は対称行列であるので直交行列 \(P\ (P^T = P^{-1})\) で

\begin{align} X^T X = P \Gamma P^T \qquad (\Gamma = {\rm diag}(\gamma_0,\ldots \gamma_D)) \end{align}

と対角化可能です。今知りたいのは \(X^T X\) の逆行列ですが、以下のように書くことができます。

\begin{align} (X^T X)^{-1} &= (P \Gamma P^T)^{-1} = (P^T)^{-1} \Gamma^{-1} P^{-1} = P \Gamma^{-1} P^T\nonumber\\ &= P {\rm diag}(1/\gamma_0, 1/\gamma_1, \ldots, 1/\gamma_D) P^T \end{align}

ここで最小の固有値がゼロである場合、 \(1/0\) となり発散してしまい逆行列が求まらないわけです。

では、正則化項を導入する( \(\alpha > 0\) )ことでどうなるのかをみてみましょう。

\begin{align} (X^T X + \alpha I)^{-1} &= (P \Gamma P^T + \alpha I)^{-1}\nonumber\\ &= \left\{ P ( \Gamma + \alpha I ) P^T \right\}^{-1}\nonumber\\ &= P ( \Gamma + \alpha I )^{-1} P^T \nonumber\\ &= P {\rm diag}\left(\frac{1}{\gamma_0 + \alpha}, \frac{1}{\gamma_1 + \alpha}, \ldots, \frac{1}{\gamma_D + \alpha}\right) P^T \end{align}

となるため、最小の固有値がゼロである場合でも \(\alpha > 0\) である限り発散せずに済むわけです。帰結として、正則化項を導入することで発散を防ぎ正則行列にすることができました。ここまでシンプルに短く正則行列であることを証明できて、最初に知った時はちょっと感動しました。

4.2 実装編

では、これまでやってきたコードで正則でない行列を作ります。具体的には計画行列に従属な関係にある別の行(または列)を作ります4。以下のように第3項と第4項を従属にし、

\begin{align} \hat{y} = \omega_0 x^0 + \omega_1 x^1 + \omega_2 x^2 + \omega_3 x^3 + \omega_4 x^4 + \omega_5 x^5 + \omega_6 (2 x^2) \end{align}

で計画行列を作ります。このような計画行列では、 \(X^T X\) でも3行目と4行目で従属な関係になるはずで、ランク落ちしており、行列式がゼロになってしまいます。仮に、説明変数にあたる \(x\) を \(200\) これまで同様生成し、 \(X^T X\) の逆行列を求めます。

# -5から5の間に一様分布からxを200個生成する
x = 10. * rand(200) - 5.
# 計画行列を作成する
# あえてランク落ちさせる
def Phi(x): return array([1, x, x**2, x**4, x**5, 2 * x**2])

def design_matrix(x, Phi): return array([Phi(i) for i in x])
# 計画行列生成!!
X = design_matrix(x, Phi)
# X^T X
X_sq = dot(X.T, X)

# 推定された係数の重みベクトル
# 特異点が出ちゃう
inv(X_sq)

お手元でお試しすればお分かりだと思いますが、

LinAlgError: Singular matrix

上記のように「特異行列になっとるから計算できん。」と頭の良いエラーが出ます。 numpy 先生が数値的に閾値を置いており、それを越えるとこのエラーが出力される設計になっていることが予想できます。

では、リッジ回帰の正則化項を導入して逆行列が問題なく出るかを確かめてみます。上記コードの最後の行を以下に置き換えるだけです。

alpha = 0.1
inv(X_sq + alpha * eye(6))

エラーにならないはずです。この逆行列を用いてリッジ回帰をしたものが以下の図になります。

f:id:pseudo-theory-of-everything:20191006162827p:plain

Figure 4: 真の関数(灰色)とランク落ちした計画行列で推定した関数(シアン)を指す曲線

問題なく推定でき、真の関数形に近い関数が予測されました。また、今回は正則化パラメータ \(\alpha = 0.1\) にしています。

さらにもう一歩踏み込んでみましょう。推定された重みベクトルは以下の通りです。

\begin{align} \vec{\hat{w}}_{\rm ridge}^T = (0.2659, 3.749, 0.06580, -0.4631, 0.00078, 0.01188, 0.1316) \end{align}

ランク落ちしているので上記、重みベクトルの第3, 7成分は従属な関係から導かれる成分のため正則化によって解けるようになるのは嬉しいのですが、どちらかが依然残っている状態は気持ち悪いです。
この状態を解決するのがスパースモデリングであり、lasso回帰(L1正則化)と呼ばれる手法です。lasso回帰を用いて推定された重みベクトルは

\begin{align} \vec{\hat{w}}_{\rm lasso}^T = (0.3222, 3.443, 0.000, -0.4186, 0.001360, 0.01048, 0.1575) \end{align}

第3成分が \(0\) となり不要な説明変数と見なされました!!このようにスパースな状態を作る手法になります。

ってなわけで予告 「スパースモデリングの世界!!」 乞うご期待です。

Footnotes:

1

歴史的には1970年にHoerlとKennardによってリッジ回帰は提案されたらしく、行列の対角成分について畝(ウネ/ridge)を作る意味でリッジ回帰と呼ばれています2。また、同様の正則化法としてlasso(least absolute shrinkage and selection operator)回帰があります。Tibshiraniによって1996年に提案されています。機械学習の正則化法として使われだしたのは案外最近なんですねーという感想。

2

個人的にはですが手法そのものはもっと大昔からあったのではと思っています

3

高次の項の係数がもし少しでもズレると、両端のデータ点から予測が大きく外れてしまい、損失が非常に大きくなってしまいます。逆に \(x=0\) 周りは低次の項の影響が強いのですが、低次の項の係数は高次の項の係数ほど感度は強くありません。結果、 \(x^{10}\) と高次の項まで回帰を考えているため、\(|x|\) の大きな値に影響されやすいです。ここでデータ点を \(+2\) 増やしているのは完全にズルをしていて、図の両端にあたる \(x=(-5,\ 5)\) に対応する真の \(y\) の値 \((11.613,\ 5.627)\) を追加しています。図からも両端の点だけ灰色の実線上にあり、結果的に回帰線(オレンジの実線)はその点を通るようにフィットされていると思います。

4

通常、計画行列にこのような仮定をしている時点で非常に筋が悪いです。