【論文紹介】E(n) Equivariant Graph Neural Networks

対称性が課された機械学習の理論に興味があり、なんとなく探していたところ、最近出た論文に読みやすそうなものがあったので読んでみました。次の論文を紹介したいと思います。

イントロダクション

この論文では、グラフニューラルネットワーク(GNN)に \(E(n)\) 変換のもとで同変(equivariant)性を課したモデルを構築しています。 \(E(n)\) は \(n\) 次元ユークリッド空間での等長変換群であり、回転、並進、鏡映、置換からなりますが、今回の論文では基本的に回転と並進に着目しているように思えます。このような変換を考えることのモチベーションとしてはData Augmentationなどがあるようで、著者たちの過去の関連論文では

arxiv.org

などがあります。後に紹介しますが、グラフニューラルネットワークに対称性を課した研究は、点群(point clouds)で表されるデータや、3次元の分子構造、N体粒子の運動シミュレーションなどを対象に行われています。ただしこれらは3次元のみに限られていたり、球面調和関数を利用するなどの少々複雑な設定が必要になっているようです [Thomas et al., 2018][Fuchs et al., 2020][Finzi et al., 2020][Köhler et al., 2020]。
この論文で提唱する方法では、従来のグラフニューラルネットワークで使われるノードの特徴ベクトル \(\boldsymbol{h}\) の他に、実際のノードの座標である \(\boldsymbol{x}\) を導入することで、シンプルに高次元への一般化を実現しています。また、この手法と従来手法での比較実験を、運動シミュレーション、グラフオートエンコーダ(GAE)を使ったグラフの再現、量子化学計算で使われる分子構造のデータセットQM9で行っています。

背景知識

ここでは同変性(equivariance)とグラフニューラルネットワーク(GNN)についてざっとですが紹介します。

同変性

群 \(G\) と \(G\) の作用する空間 \(X\) と \(Y\) を考えます。 \(g \in G\) による \(X,Y\) の変換をそれぞれ\(T_g : X \rightarrow X\), \(S_g : Y \rightarrow Y\) とします。関数 \(\phi : X \rightarrow Y\) が \(g\) について同変であるとは、以下を満たすことを言います：

\begin{align}
\phi \left( T_g(\boldsymbol{x}) \right) = S_g \left( \phi (\boldsymbol{x}) \right)
\end{align}

この論文では、 \(\boldsymbol{x}\) を粒子の座標と考えて、以下の3つの変換に対する同変性を考えます。

1. 並進 : \(\boldsymbol{g} \in \mathbb{R}^n\) に対して \(\boldsymbol{y} + \boldsymbol{g} = \phi(\boldsymbol{x} + \boldsymbol{g})\)
2. 回転 : 直交行列 \(Q \in O(n)\) に対して \(Q\boldsymbol{y} = \phi(Q\boldsymbol{x})\)
3. 置換 : \(P\) を \(\boldsymbol{x} = (\boldsymbol{x}_1, \ldots, \boldsymbol{x}_M)\) に作用する置換と考えて、 \(P(\boldsymbol{y}) = \phi(P(\boldsymbol{x}))\)

グラフニューラルネットワーク

f:id:pseudo-theory-of-everything:20210604210902p:plain — グラフニューラルネットワークのイメージ図

グラフ \(\cal{G} = (\cal{V}, \cal{E})\) ( \(\cal{V}\) はノード \(v_i\) の集合、 \(\cal{E}\) はエッジ \(e_{ij}\) の集合)を考えます。
グラフ畳み込み層を次の式で定義します。 [Gilmer et al., 2017]

\begin{align}
\boldsymbol{m}_{ij} &= \phi_e (\boldsymbol{h}^l_i, \boldsymbol{h}^l_j, a_{ij})\\
\boldsymbol{m}_i &= \sum_{j \in {\cal N}(i)} \boldsymbol{m}_{ij}\\
\boldsymbol{h}^{l+1}_i &= \phi_h(\boldsymbol{h}^l_i, \boldsymbol{m}_i)
\end{align}

ただし、 \(\boldsymbol{h}^l_i\) は第 \(l\) 層でのノード \(v_i\) の埋め込み、 \(a_{ij}\) はエッジの持つ属性、 \({\cal N}(i)\) はノード \(v_i\) の隣接ノードの集合を表します。また、 \(\phi_e, \phi_h\) はそれぞれエッジとノードに作用する関数で、一般的にはこれを多層パーセプトロンで近似します。

同変グラフニューラルネットワーク

この論文で提唱する、同変グラフニューラルネットワーク(Equivariant Graph Neural Networks:EGNNs)を定義します。ポイントとしては、上で定義したグラフニューラルネットワークで使ったものに加え、グラフを実際に \(n\) 次元空間中で表現した時のノードの座標 \(\boldsymbol{x}_i \in \mathbb{R}^n\) を導入することです。グラフの \(E(n)\) 変換はこの座標 \(\boldsymbol{x}\) に作用する形で記述されます。

グラフ畳み込み層のように、同変グラフ畳み込み層(Equivariant Graph Convolutional Layer : EGCL)を定義します。EGCLは、第 \(l\) 層からの入力として、ノードの埋め込み \(\boldsymbol{h}^l=\{\boldsymbol{h}^l_0,\ldots,\boldsymbol{h}^l_{M - 1}\}\) 、
座標 \(\boldsymbol{x}^l=\{\boldsymbol{x}^l_0,\ldots,\boldsymbol{x}^l_{M -1 }\}\) 、
エッジの集合 \({\cal E}\) を与えて、第 \(l+1\) 層の出力 \(\boldsymbol{h}^{l+1}, \boldsymbol{x}^{l+1}\) を返すものと考え、形式的にこれを \(\boldsymbol{h}^{l+1}, \boldsymbol{x}^{l+1} =\) EGCL[ \(\boldsymbol{h}^l, \boldsymbol{x}^l, {\cal E}\) ]と表します。
EGCLは以下の式で定義されます。

\begin{align}
\boldsymbol{m}_{ij} &= \phi_e(\boldsymbol{h}^l_i, \boldsymbol{h}^l_j,\|\boldsymbol{x}^l_i - \boldsymbol{x}^l_j\|^2, a_{ij})\\
\boldsymbol{x}^{l+1}_i &= \boldsymbol{x}^l_i + \frac{1}{M - 1}\sum_{j \neq i}(\boldsymbol{x}^l_i - \boldsymbol{x}^l_j) \phi_x(\boldsymbol{m}_{ij})\\
\boldsymbol{m}_i &= \sum_{j \in {\cal N}(i)} \boldsymbol{m}_{ij}\\
\boldsymbol{h}^{l+1}_i &= \phi_h(\boldsymbol{h}^l_i, \boldsymbol{m}_i)
\end{align}

グラフ畳み込み層との大きな違いは座標 \(\boldsymbol{x}^{l+1}_i\) の導入と、隣接ノードの情報を集約した \(\boldsymbol{m}_{ij}\) にノード間の距離の情報が取り入れられたことです。座標の更新式を見てみると、元のノードの位置に対して、隣接ノードの相対位置 \((\boldsymbol{x}^l_i - \boldsymbol{x}^l_j)\) の重み付き和が補正として入る形になっています。その重みもノードの埋め込みによる隣接ノードの情報を取り入れたスカラー \(\phi_x(\boldsymbol{m}_{ij})\) で与えられます。

\(\phi_e, \phi_x, \phi_h\) はそれぞれ多層パーセプトロンで与えられます。問題によってこの多層パーセプトロンの組み方を変えることが可能なようですが、論文内で実際に使われたのは以下の構成になります。

\(\phi_e\) : Input \(\rightarrow\) {LinearLayer() \(\rightarrow\) Swish() \(\rightarrow\) LinearLayer() \(\rightarrow\) Swhish()} \(\rightarrow\) Output
\(\phi_x\) : \(\boldsymbol{m}_{ij}\) \(\rightarrow\) {LinearLayer() \(\rightarrow\) Swish() \(\rightarrow\) LinearLayer()} \(\rightarrow\) Output
\(\phi_h\) : [ \(\boldsymbol{h}^l_i, \boldsymbol{m}_i\) ] \(\rightarrow\) {LinearLayer() \(\rightarrow\) Swish() \(\rightarrow\) LinearLayer() \(\rightarrow\) Addition( \(\boldsymbol{h}^l_i\) )} \(\rightarrow\) \(\boldsymbol{h}^{l+1}_i\)

\(E(n)\) 同変性の確認

定義した同変グラフ畳み込み層(EGCL)が並進、回転に対して同変性を持つことを確認します。つまり、ベクトル \(\boldsymbol{g} \in \mathbb{R}^n\) と直交行列 \(Q \in O(n)\) が与えられた時、以下の式が満たされることを確認します。

\begin{align}
Q \boldsymbol{x}^{l+1} + \boldsymbol{g}, \boldsymbol{h}^{l+1}
= \mbox{EGCL}[Q \boldsymbol{x}^l + \boldsymbol{g}, \boldsymbol{h}^l]
\end{align}

定義より \(\boldsymbol{m}_{ij}\) が回転・並進に対して不変であることはわかるので、 \(\boldsymbol{h}^{l+1}_i\) も不変であることはわかります。 \(\boldsymbol{x}^{l+1}_i\) の更新式にはあらわに \(\boldsymbol{x}^l\) が使われているので、変換式に従って計算を追ってみます。

\begin{align*}
\boldsymbol{x}^{l+1}_i \rightarrow
& (Q \boldsymbol{x}^l_i + \boldsymbol{g})
+ \frac{1}{M - 1}\sum_{i \neq j}
\left\{
(Q \boldsymbol{x}^l_i + \boldsymbol{g})
- (Q \boldsymbol{x}^l_j + \boldsymbol{g})
\right\}\phi_x(\boldsymbol{m}_{ij})\\
& = Q \left\{
\boldsymbol{x}^l_i + \frac{1}{M - 1}\sum_{i \neq j}
(\boldsymbol{x}^l_i - \boldsymbol{x}^l_j) \phi_x(\boldsymbol{m}_{ij})
\right\} + \boldsymbol{g}\\
& = Q \boldsymbol{x}^{l+1}_i + \boldsymbol{g}
\end{align*}

以上より、EGCLが \(E(n)\) 同変であることが確認できます。置換は大丈夫なのか、と思ったのですが、おそらく対象としているデータがそもそもノードの入れ替えに対して不変なものを扱っているのだと思います……

ノードが速度を持つ場合への拡張

運動シミュレーションなどへの応用で、ノードに対応する粒子が速度を持っている問題を考えたい場合があります。この時、ノードの位置 \(\boldsymbol{x}^l_i\) は速度によって更新されるため、新たに速度ベクトル \(\boldsymbol{v}^l_i\) を導入し、 \(\boldsymbol{x}^l_i\) の更新式を次の2式に変更します。

\begin{align}
\boldsymbol{v}^{l+1}_i
&= \phi_v(\boldsymbol{h}^l_i)\boldsymbol{v}^l_i
+ \frac{1}{M - 1}\sum_{j \neq i}
(\boldsymbol{x}^l_i - \boldsymbol{x}^l_j) \phi_x(\boldsymbol{m}_{ij}) \\
\boldsymbol{x}^{l+1}_i
&= \boldsymbol{x}^l_i + \boldsymbol{v}^{l+1}_i
\end{align}

ただし、 \(\phi_v : \mathbb{R}^N \rightarrow \mathbb{R}\) はノードの埋め込みからスケールを与える関数であり、これも多層パーセプトロンで与えます。

実験

この論文では

1. N体粒子の運動シミュレーション
2. グラフオートエンコーダー(GAE)
3. 分子のデータセットQM9を使った物性予測

の3つのタスクに関して既存手法との比較実験を行っています。この内グラフオートエンコーダ(GAE)の実験について紹介します。
(GAEについての参考ページ)

www.yuyakaneta.page

問題設定

GAEは隣接行列 \(A\) とノードの特徴を入力とし潜在空間での表現 \(\boldsymbol{z}\) を推論し、求めた潜在変数から予測した隣接行列 \(\hat{A}\) が元の \(A\) に近づくように学習させる手法です[Kipf & Welling, 2016]。

今回の実験で行うのは、[Liu et al., 2019]で提示された、潜在空間の座標 \(\boldsymbol{z}\) から隣接行列を再現するdecorder関数

\begin{align}
\hat{A}_{ij} = g_e(\boldsymbol{z}_i,\boldsymbol{z}_j)
= \frac{1}{1+\exp(w||\boldsymbol{z}_i - \boldsymbol{z}_j||^2 + b)}
\end{align}

を使い、EGNNがどれだけ隣接行列を再現できるかを確かめます。
比較手法と大きく違う点として、先に述べたようにEGNNはノード埋め込み(ノードの特徴を表すベクトル) \(\boldsymbol{h}\) と位置 \(\boldsymbol{x}\) の2つを更新している事が挙げられます。このとき、潜在変数 \(\boldsymbol{z}\) に何を使うか、ということになりますが、EGNNでは埋め込み \(\boldsymbol{h}\) を使わず \(\boldsymbol{x}\) だけで再現するタスクとします。

データセット

以下の2つの異なるモデルからグラフを生成し、それぞれトレーニングに5000、バリデーションに500、テストに500個のグラフを使用しました。

[You et al.,2018]で提案された手法を使い生成したグラフ
- ノード数 \(12 \leq M \leq 20\)
Erdos-Renyi生成モデルを使いサンプリングしたグラフ
- 初期ノード数 \(7 \leq M \leq 16\) 、エッジ生成確率 \(p_e = 0.25\)

実験結果

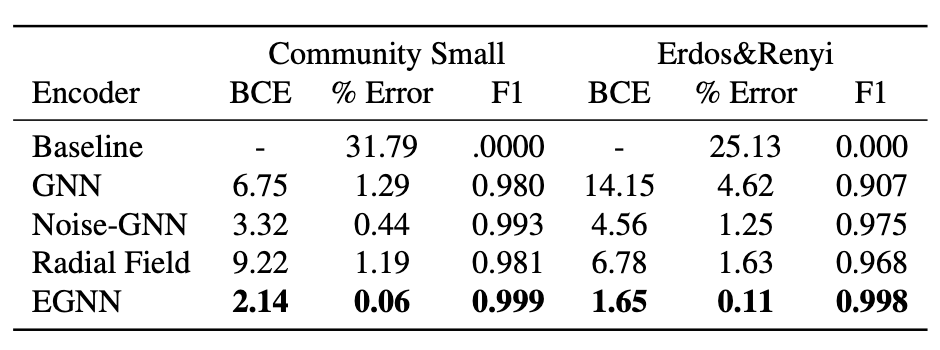
f:id:pseudo-theory-of-everything:20210604210934p:plain — 表2

実験結果をまとめたものが表2になります(論文のFigure5から引用)。比較手法はベースラインモデル(隣接行列の全成分がゼロ \(\hat{A}_{ij}=0\) )、GNN、Noise-GNN(ノードの埋め込みに正規分布でノイズを与えたモデル)、Radial Fieldになります。
それぞれ比較している数値は、

Binary cross entropy(BCE): \({\cal L}=\sum_{i,j}BCE(\hat{A}_{ij}, A_{ij})\)
% Error: 予測したエッジのうち、間違っていたものの割合
F1スコア

となります。どちらのグラフでも良い結果を出していることがわかります。これだけでもスコアが良いのでメリットとは言えるのですが、隣接行列を再現するにあたってsymmetry problem と呼ばれる問題があり、この問題に対する対処が楽だということもメリットとして挙げられています。

Conclusions

\(E(n)\) 同変であるグラフニューラルネットワークの新しいアーキテクチャーを提案しました
既存の手法と比べ、複雑な関数を導入しない、任意の次元への適用が可能という利点があります
具体的な課題に対する実験において既存の手法と比較し良いスコアが出ることを確かめました

Pseudo Theory of Everything

データサイエンス初心者物理学徒の奮闘記